Как делить десятичные дроби на натуральное. Устремишь с вниманьем взгляд

Деление десятичной дроби на натуральное число

Как выполнить деление десятичной дроби на натуральное число? Запишем правило и рассмотрим его применение на примерах.

При делении десятичной дроби на натуральное число:

1) делим, не обращая внимания на запятую;

2) когда заканчивается деление целой части, в частном ставим запятую.

Если целая часть делимого меньше делителя, то целая часть частного равна нулю.

Примеры деления десятичных дробей на натуральные числа.

Делим, не обращая внимания на запятую, то есть 348 делим на 6. При делении 34 на 6 берём по 5. 5∙6=30, 34-30=4, то есть остаток равен 4.

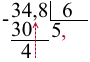
Отличие деления десятичной дроби на натуральное число от деления целых чисел только в том, что, когда деление целой части закончилось, в частном ставим запятую. То есть при переходе через запятую, прежде чем снести к остатку от деления целой части, 4, число 8 из дробной части, в частном пишем запятую.

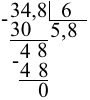Сносим 8. 48_6=8. В частное пишем 8.

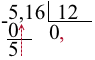2) 5,16:12=?

Так как 5 на 12 не делится, в частном пишем нуль. Деление целой части окончено, в частном ставим запятую.

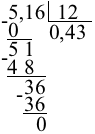
Сносим 1. При делении 51 на 12 берём по 4. В остатке — 3.

Таким образом, 5,16:12=0,43.

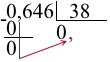3) 0,646:38=?

В целой части делимого стоит нуль. Так как нуль на 38 не делится, в частном ставим 0. Деление целой части окончено, в частном пишем запятую.

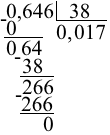
Сносим 6. Так как 6 на 38 не делится, в частном пишем ещё один нуль.

Сносим 4. При делении 64 на 38 берём по 1. В остатке — 26.

Сносим 6. 266_38=7.

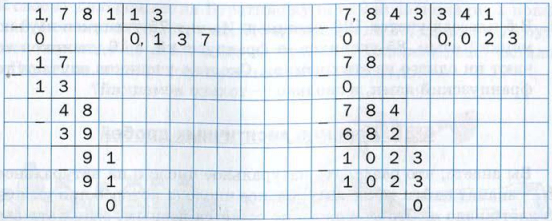
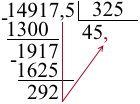4) 14917,5:325=?

При делении 1491 на 325 берём по 4. В остатке получаем 191. Сносим 7. При делении 1917 на 325 берём по 5. Остаток — 292.

Поскольку деление целой части закончено, в частном пишем запятую.

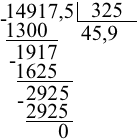
Сносим 5. 2925_325=9.

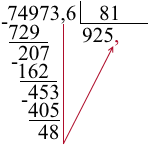5) 74973,6:81=?

При делении 749 на 81 берём по 9. Остаток — 20.

Сносим 7. При делении 207 на 81 берём по 2. Остаток — 45.

Сносим 3. При делении 453 на 81 берём по 5. В остатке — 48. Так как деление целой части окончено, в частном ставим запятую.

Деление десятичных дробей на натуральные числа – Урок 2 – УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ – ДРОБНЫЕ ЧИСЛА

Основная дидактическая цель урока: продолжить работу над формированием умения выполнять деление десятичных дробей на натуральные числа.

I. Организационный момент

II. Определение темы урока

Сегодня на уроке мы будем продолжать учиться выполнять деление десятичной дроби на натуральное число. Вспомним приемы проверки действия деления.

III. Устный счет

Если ты на эти числа

Устремишь с вниманьем взгляд,

То найдешь закономерность

И продолжишь чисел ряд.

Фронтальная работа (учащиеся работают вместе с учителем).

а) 1,2; 1,8; 2,4; 3;. (3,6; 4,2.) (Закономерность состоит в том, Что к каждому числу для получения следующего прибавляется 0,6.)

б) 9,6; 8,9; 8,2; 7,5. (6,8; 6,1.) (Каждое следующее число получается вычитанием из предыдущего 0,7.)

в) 0,9; 1,8; 3,6; 7,2. (14,4; 28,8.) (Каждое следующее число получается путем умножения предыдущего на 2.)

г) 1,2; 0,7; 2,2; 1,4; 3,2; 2,1. (4,2; 2,8.) (Рассмотрим первое, третье и пятое число — видим, что каждое следующее у них на единицу больше, значит, седьмое число — 4,2. Рассмотрим второе, четвертое и шестое — каждое следующее увеличивается на 0,7. Значит, восьмое число — 2,8.)

IV. Самостоятельная работа

КИМы: проверочный тест 31 по теме “Десятичные дроби. Умножение и деление десятичных дробей”.

V. Работа по теме урока

1. На доске: 33,06 : 95 = 0,348

— Как определить, верно ли найдено значение выражения? (Сделать проверку.)

Деление выполняется уголком, проверка — с использованием записи в столбик.

2. С. 211, № 1358 (интерактивное пособие).

VI. Работа над задачами

1. С. 210, № 1342 (работа в паре).

1) 6,6 ∙ 12 = 79,2 (см 2 ) — площадь первого прямоугольника.

2) 79,2 : 11 = 7,2 (см 2 ) — площадь второго прямоугольника.

3) 7,2 : 8 = 0,9 (см) — ширина второго прямоугольника.

2. С. 210, № 1343 (самостоятельно).

(При проверке рассматриваются два способа решения.)

1) 25,2 : 7 ∙ 3 = 7,2 (км) — прошел турист в первый день.

2) 25,2 — 7,2 = 18 (км) — прошел турист во второй день.

1) — такая часть пути пройдена туристом во второй день.

2) 25,2 : 7 ∙ 4 = 18 (км) — прошел турист во второй день.

— Прочитайте задачу. Сравните ее с предыдущей.

— Решите ее самостоятельно любым способом.

1) 36,9 : 9 ∙ 7 = 28,7 (т) — отправили на консервный завод.

2) 36,9 — 28,7 = 8,2 (т) — продано населению.

Деление натуральных дробей

Вы знаете, что разделить натуральное число a на натуральное число b − значит найти такое натуральное число c, которое при умножении на b дает число a. Это утверждение остается верным, если хотя бы одно из чисел a, b, c является десятичной дробью.

Рассмотрим несколько примеров, в которых делителем является натуральное число.

1,2 : 4 = 0,3 , так как 0,3 * 4 = 1,2 ;

2,5 : 5 = 0,5 , так как 0,5 * 5 = 2,5 ;

1 : 2 = 0,5 , так как 0,5 * 2 = 1 .

А как быть в тех случаях, когда деление не удается выполнить устно?

Например, как разделить 43,52 на 17 ?

Увеличив делимое 43,52 в 100 раз, получим число 4 352 . Тогда значение выражения 4 352 : 17 в 100 раз больше значения выражения 43,52 : 17 . Выполнив деление уголком, вы легко установите, что 4 352 : 17 = 256 . Здесь делимое увеличено в 100 раз. Значит, 43,52 : 17 = 2,56 . Заметим, что 2,56 * 17 = 43,52 , что подтверждает правильность выполнения деления.

Частное 2,56 можно получит иначе. Будем делить 4352 на 17 уголком, не обращая внимания на запятую. При этом запятую в частном следует поставить непосредственно перед тем, как будет использована первая цифра после запятой в делимом:

Если делимое меньше делителя, то целая часть частного равна нулю. Например:

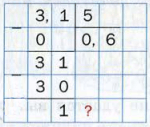
Рассмотрим еще один пример. Найдем частное 3,1 : 5 . Имеем:

Мы остановили процесс деления, потому что цифры делимого закончились, а в остатке нуль не получили. Вы знаете, что десятичная дробь не изменится, если к ней справа приписать любое количество нулей. Тогда становится понятным, что цифры делимого закончиться не могут. Имеем:

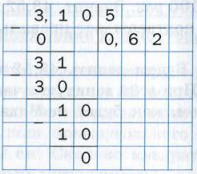
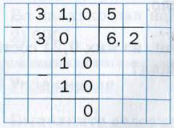
Теперь мы можем находить частное двух натуральных чисел, когда делимое не делится нацело на делитель. Например, найдем частное 31 : 5 . Очевидно, что число 31 не делится нацело на 5 :

Мы остановили процесс деления, потому что цифры делимого закончились. Однао если представить делимое в виде десятичной дроби, то деление можно продолжить.

Имеем: 31 : 5 = 31,0 : 5 . Далее выполним деление уголком:

Следовательно, 31 : 5 = 6,2 .

В предыдущем параграфе мы выяснили, что если запятую перенести вправо на 1, 2, 3 и т.д. цифры, то дробь увеличится соответственно в 10, 100, 1 000 и т. д. раз, а если запятую перенести влево на 1, 2, 3 и т. д. цифры, то дробь уменьшится соответственно в 10, 100, 1 000 и т. д. раз.

Поэтому в тех случаях, когда делитель равен 10, 100, 1 000 и т. д., пользуются следующим правилом.

Чтобы разделить десятичную дробь на 10, 100, 1 000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.

Например: 4,23 : 10 = 0,423 ; 2 : 100 = 0,02 ; 58,63 : 1 000 = 0,05863 .

Итак, мы научились делить десятичную дробь на натуральное число.

Покажем, как деление на десятичную дробь можно свести к делению на натуральное число.

Этот пример иллюстрирует следующее: если делимое и делитель увеличить одновременно в 10, 100, 1 000 и т.д. раз, то частное не изменится.

Найдем частное 43,52 : 1,7 .

Увеличим одновременно делимое и делитель в 10 раз. Имеем:

43,52 : 1,7 = 435,2 : 17 .

Увеличим одновременно делимое и делитель в 10 раз. Имеем: 43,52 : 1,7 = 25,6 .

Чтобы разделить десятичную дробь на десятичную надо:

1 ) перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;

2 ) выполнить деление на натуральное число.

Пример 1 . Ваня собрал 140 кг яблок и груш, из них 0,24 составляли груши. Сколько килограммов груш собрал Ваня?

1 ) 140 : 100 = 1,4 (кг) − составляет

2 ) 1,4 * 24 = 33,6 (кг) − груш было собрано.

Пример 2 . На завтрак Винни−Пух съел 0,7 бочонка меда. Сколько килограммов меда было в бочонке, если Винни−Пух съел 4,2 кг?

1 ) 4,2 : 7 = 0,6 (кг) − составляет

2 ) 0,6 * 10 = 6 (кг) −меда было в бочонке.

Источники:

http://www.for6cl.uznateshe.ru/delenie-desyatichnoj-drobi-na-naturalnoe-chislo/
http://compendium.su/mathematics/5klass/119.html
http://reshalka.com/glossaries/54