Определение что такое простые числа. Как найти простые числа

Алгоритмы нахождения простых чисел

Простые числа – это натуральные числа, большие единицы, которые имеют только два делителя: единицу и само это число.

Примеры простых чисел: 2 , 3, 5, 7, 11, 13…

(Единица не является простым числом!)

Существует множество задач, связанных с простыми числами, и хотя формулируются они достаточно просто, решить их бывает очень трудно. Некоторые свойства простых чисел еще не открыты. Это побудило немецкого математика Германа Вейля (Wayl, 1885-1955) так охарактеризовать простые числа: «Простые числа – это такие существа, которые всегда склонны прятаться от исследователя».

Во все времена люди хотели найти как можно большее простое число. Пока люди считали только при помощи карандаша и бумаги, им нечасто удавалось обнаружить новые простые числа. До 1952 г. самое большое известное простое число состояло из 39 цифр. Теперь поиском все больших простых чисел занимаются компьютеры. Это может представлять интерес для любителей рекордов.

Не будем гнаться за рекордами, а рассмотрим несколько алгоритмов нахождения простых чисел.

Задача 1. Определение простого числа.

Составить программу, которая будет проверять, является ли введенное число простым.

Самый простой путь решения этой задачи – проверить, имеет ли данное число n (n >= 2) делители в интервале [2; n-1]. Если делители есть, число n – составное, если – нет, то – простое. При реализации алгоритма разумно делать проверку на четность введенного числа, поскольку все четные числа делятся на 2 и являются составными числами, то, очевидно, что нет необходимости искать делители для этих чисел. Логическая переменная flag в программе выступает в роли “флаговой” переменной и повышает наглядность программы, так, если flag = true, то n –простое число; если у числа n есть делители, то “флаг выключаем” с помощью оператора присваивания flag:= false, таким образом, если flag = false, то n – составное число.

Задача 2. Нахождение простых чисел в заданном интервале.

Составить программу, которая напечатает все простые числа в заданном интервале [2, m], для m>3 и подсчитает их количество.

Для реализации данного алгоритма необходимо проверить каждое число, находящееся в данном интервале, – простое оно или нет. Однако для этого машине пришлось бы потратить много времени. Поэтому подумаем, каким образом можно оптимизировать алгоритм, описанный в задаче 1, применительно к задаче 2?

Будем использовать следующие приемы оптимизации алгоритма:

1. рассматривать только нечетные числа;
2. использовать свойство: наименьшее число, на которое делится натуральное число n, не превышает целой части квадратного корня из числа n;
3. прерывать работу цикла, реализующего поиск делителей числа, при нахождении первого же делителя с помощью процедуры Break, которая реализует немедленный выход из цикла и передает управление оператору, стоящему сразу за оператором цикла.

Как правило, учащиеся сами догадываются о приемах №1 и №3, но не всегда знают, как реализовать в программе досрочное завершение цикла, прием же №2 для них не очевиден, поэтому, возможно, учителю следует остановиться на нем более подробно или же привести полное доказательство этого утверждения.

Счетчик чисел будет находиться в переменной k. Когда очередное простое число найдено, он увеличивается на 1. Простые числа выводятся по 10 в строке, как только значение счетчика становится кратным 10, курсор переводится на новую строку.

Близнецы

Два нечетных простых числа, разнящихся на два, называются близнецами. Близнецами являются, например, числа 5 и 7, 11 и 13, 17 и 19 и т.д. В начале натурального ряда такие пары чисел встречаются достаточно часто, но, по мере того как мы продвигаемся в область больших чисел, их становится все меньше и меньше. Известно, что в первой сотне имеется целых 8 близнецов, дальше они расположены очень неравномерно, их можно обнаружить все реже и реже, гораздо реже, нежели сами простые числа. До сих пор неясно, конечно ли число близнецов. Более того, еще не найден способ, посредством которого можно было бы разрешить эту проблему.

Задача 3. Поиск пар чисел близнецов.

Написать программу, которая будет находить все числа близнецы в интервале [2; 1000] и подсчитывать количество пар чисел близнецов.

Фактически будем использовать алгоритм и программу Задачи 2. В этом алгоритме нужно использовать дополнительные переменные для хранения двух “последних” простых чисел и проверять условие наличия близнецов – их разность должна быть равна двум.

Задача 4. Нахождение простых чисел в заданном интервале с выводом в выходной файл.

Реализовать алгоритм задачи 2 с выводом простых чисел в выходной файл по 10 в строке. Последняя строка файла должна содержать информацию о количестве простых чисел в заданном интервале.

Задача 5. Приемы оптимизации алгоритма задачи 4.

Оптимизировать алгоритм задачи 4 следующим образом: найденные простые числа записывать в файл, делимость очередного кандидата проверять только на числа из этого файла.

Словесное описание алгоритма:

1. Вводим правую границу диапазона – m;
2. Записываем двойку и тройку в файл;
3. Пока очередное нечетное число i m ), вывести в файл количество простых чисел.

Эратосфеново решето

Греческий математик Эратосфен (275-194 гг. до н.э.) предложил интересный метод нахождения простых чисел в интервале [2; n]. Он написал на папирусе, натянутом на рамку, все числа от 2 до 10000 и прокалывал составные числа. Папирус стал, как решето, которое “просеивает” составные числа, а простые оставляет. Поэтому такой метод называется Эратосфеновым решетом. Рассмотрим подробнее этот метод.

Пусть написаны числа от 2 до n:

2 3 4 5 6 7 8 9 10 11 12 . . .

Первое неперечеркнутое число в строке является простым. Таким образом, 2 – простое число. Начинаем “просеивание” с него, перечеркивая все числа, которые делятся на 2:

Далее берем следующее по порядку неперечеркнутое число и перечеркиваем все числа, кратные ему и т. д. Таким образом, мы перечеркнем все составные числа, а простые останутся неперечеркнутыми:

Все числа указанного интервала можно рассматривать как множество и в дальнейшем из этого множества будем исключать (отсеивать) все составные числа.

Задача 6. Нахождение простых чисел с помощью решета Эратосфена.

Реализовать алгоритм решета Эратосфена с помощью организации работы с множествами.

Словесное описание алгоритма:

1. Выделим из первых n натуральных чисел все простые числа (решето Эратосфена).
2. Вначале формируем множество BeginSet, состоящее из всех целых чисел в диапазоне от 2 до n. Множество PrimerSet будет содержать искомые простые числа.
3. Затем циклически повторим действия:
   1. взять из BeginSet первое входящее в него число next и поместить его в PrimerSet;
   2. удалить из BeginSet число next и все другие числа, кратные ему, т. е. 2* next, 3* next и т. д.

Цикл повторяется до тех пор, пока множество BeginSet не станет пустым. Программу нельзя использовать для произвольного n, т. к. в любом множестве не может быть больше 256 элементов. (Для расширения интервала простых чисел можно разбить одно большое множество на несколько маленьких, т. е. представить большое множество в виде массива малых множеств. Этот случай рассматривать не будем. Можно предложить наиболее заинтересованным учащимся самостоятельно рассмотреть этот вариант.)

Литература:

1. Е.В. Андреева Методика обучения основам программирования на уроках информатики. Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006.
2. В.А. Дагене, Г.К. Григас, А.Ф. Аугутис 100 задач по программированию. – М.: Просвещение, 1993. – 255 с.
3. В.В. Фаронов Турбо Паскаль 7.0. Начальный курс. Учебное пособие. – М.: «Нолидж», 1999. – 616 с.

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Простыми числами называют целые числа, которые больше единицы и имеют два положительных делителя, то есть себя и 1 .

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Составное число – это натуральное число, имеющее более двух положительных делителей.

Любое число, которое больше 1 является либо простым, либо составным. Из свойства делимости имеем, что 1 и число а всегда будут делителями для любого числа а , то есть оно будет делиться само на себя и на 1 . Дадим определение целых чисел.

Натуральные числа, которые не являются простыми, называют составными.

Простые числа: 2 , 3 , 11 , 17 , 131 , 523 . Они делятся только сами на себя и на 1 . Составные числа: 6 , 63 , 121 , 6697 . То есть число 6 можно разложить на 2 и 3 , а 63 на 1 , 3 , 7 , 9 , 21 , 63 , а 121 на 11 , 11 , то есть его делители будут 1 , 11 , 121 . Число 6697 разложится на 37 и 181 . Заметим, что понятия простых чисел и взаимно простых чисел – разные понятия.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Таблица для всех существующих натуральных чисел нереальна, так как их существует бесконечное множество. Когда числа достигают размеров 10000 или 1000000000 , тогда следует задуматься об использовании решета Эратосфена.

Рассмотрим теорему, которая объясняет последнее утверждение.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Возьмем, что а является натуральным числом, которое больше 1 , b является наименьшим отличным от единицы делителем для числа а . Следует доказать, что b является простым числом при помощи метода противного.

Допустим, что b – составное число. Отсюда имеем, что есть делитель для b , который отличен от 1 как и от b . Такой делитель обозначается как b 1 . Необходимо, чтобы условие 1 b 1 b было выполнено.

Из условия видно, что а делится на b , b делится на b 1 , значит, понятие делимости выражается таким образом: a = b · q и b = b 1 · q 1 , откуда a = b 1 · ( q 1 · q ) , где q и q 1 являются целыми числами. По правилу умножения целых чисел имеем, что произведение целых чисел – целое число с равенством вида a = b 1 · ( q 1 · q ) . Видно, что b 1 – это делитель для числа а . Неравенство 1 b 1 b не соответствует, потому как получим, что b является наименьшим положительным и отличным от 1 делителем а .

Простых чисел бесконечно много.

Предположительно возьмем конечное количество натуральных чисел n и обозначим как p 1 , p 2 , … , p n . Рассмотрим вариант нахождения простого числа, отличного от указанных.

Примем на рассмотрение число р, которое равняется p 1 , p 2 , … , p n + 1 . Оно не равняется каждому из чисел, соответствующих простым числам вида p 1 , p 2 , … , p n . Число р является простым. Тогда считается, что теорема доказана. Если оно составное, тогда нужно принять обозначение p n + 1 и показать несовпадение делителя ни с одним из p 1 , p 2 , … , p n .

Если это было бы не так, тогда, исходя из свойства делимости произведения p 1 , p 2 , … , p n _, получим, что оно делилось бы на p n + 1 . Заметим, что на выражение p n + 1 делится число р равняется сумме p 1 , p 2 , … , p n + 1 . Получим, что на выражение p n + 1 должно делиться второе слагаемое этой суммы, которое равняется 1 , но это невозможно.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Так как простых чисел очень много, то таблицы ограничивают числами 100 , 1000 , 10000 и так далее.

Решето Эратосфена

При составлении таблицы простых чисел следует учитывать то, что для такой задачи необходима последовательная проверка чисел, начиная с 2 до 100 . При отсутствии делителя оно фиксируется в таблицу, если оно составное, то в таблицу не заносится.

Если начать с числа 2 , то оно имеет только 2 делителя: 2 и 1, значит, его можно занести в таблицу. Также и с числом 3 . Число 4 является составным, следует разложить его еще на 2 и 2 . Число 5 является простым, значит, можно зафиксировать в таблице. Так выполнять вплоть до числа 100 .

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Способ при помощи решета Эратосфена считают самым удобным. Рассмотрим на примере таблиц, приведенных ниже. Для начала записываются числа 2 , 3 , 4 , … , 50 .

Теперь необходимо зачеркнуть все числа, которые кратны 2 . Произвести последовательное зачеркивание. Получим таблицу вида:

Далее вычеркиваем все числа, кратные 3 . Получаем таблицу вида:

Переходим к вычеркиванию чисел, кратных 5 . Получим:

Вычеркиваем числа, кратные 7 , 11 . В конечном итоге таблица получает вид

Перейдем к формулировке теоремы.

Наименьший положительный и отличный от 1 делитель основного числа а не превосходит a , где a является арифметическим корнем заданного числа.

Необходимо обозначить b наименьший делитель составного числа а . Существует такое целое число q , где a = b · q , причем имеем, что b ≤ q . Недопустимо неравенство вида b > q , так как происходит нарушение условия. Обе части неравенства b ≤ q следует умножить на любое положительное число b , не равное 1 . Получаем, что b · b ≤ b · q , где b 2 ≤ a и b ≤ a .

Из доказанной теоремы видно, что вычеркивание чисел в таблице приводит к тому, что необходимо начинать с числа , которое равняется b 2 и удовлетворяет неравенству b 2 ≤ a . То есть, если вычеркнуть числа, кратные 2 , то процесс начинается с 4 , а кратных 3 – с 9 и так далее до 100 .

Составление такой таблицы при помощи теоремы Эратосфена говорит о том, что при вычеркивании всех составных чисел, останутся простые, которые не превосходят n . В примере, где n = 50 , у нас имеется, что n = 50 . Отсюда и получаем, что решето Эратосфена отсеивает все составные числа, которые по значению не больше значения корня из 50 . Поиск чисел производится при помощи вычеркивания.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Доказать что число 898989898989898989 является составным.

Сумма цифр заданного числа равняется 9 · 8 + 9 · 9 = 9 · 17 . Значит, число 9 · 17 делится на 9 , исходя из признака делимости на 9 . Отсюда следует, что оно составное.

Такие признаки не способны доказать простоту числа. Если нужна проверка, следует производить другие действия. Самый подходящий способ – это перебор чисел. В течение процесса можно найти простые и составные числа. То есть числа по значению не должны превосходить a . То есть число а необходимо разложить на простые множители. если это будет выполнено, тогда число а можно считать простым.

Определить составное или простое число 11723 .

Теперь необходимо найти все делители для числа 11723 . Необходимо оценить 11723 .

Отсюда видим, что 11723 200 , то 200 2 = 40 000 , а 11 723 40 000 . Получаем, что делители для 11 723 меньше числа 200 .

Для более точной оценки числа 11723 необходимо записать выражение 108 2 = 11 664 , а 109 2 = 11 881 , то 108 2 11 723 109 2 . Отсюда следует, что 11723 109 . Видно, что любое число, которое меньше 109 считается делителем для заданного числа.

При разложении получим, что 2 , 3 , 5 , 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 , 47 , 53 , 59 , 61 , 67 , 71 , 73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 – это все простые числа. Весь данный процесс можно изобразить как деление столбиком. То есть разделить 11723 на 19 . Число 19 является одним из его множителей, так как получим деление без остатка. Изобразим деление столбиком:

Отсюда следует, что 11723 является составным числом, потому как кроме себя и 1 имеет делитель 19 .

Ответ: 11723 является составным числом.

Как найти простые числа?

Числа бывают разными: натуральными, естественными, рациональными, целыми и дробными, положительными и отрицательными, комплексными и простыми, нечетными и четными, действительными и др. Из данной статьи можно узнать, что такое простые числа.

Какие числа называют английским словом “симпл”?

Очень часто школьники на один из самых несложных на первый взгляд вопросов математики, о том что такое простое число, не знают, как ответить. Они часто путают простые числа с натуральными (то есть числа, которые используются людьми при счете предметов, при этом в некоторых источниках они начинаются с нуля, а в других – с единицы). Но это совершенно два разных понятия. Простые числа – это, натуральные, то есть целые и положительные числа, которые большее единицы и которые имеют всего лишь 2 натуральных делителя. При этом один из этих делителей – это данное число, а второй – единица. Например, три – это простое число, поскольку он не делится без остатка ни на какое другое число, кроме себя самого и единицы.

Составные числа

Противоположностью простых чисел являются составные. Они также являются натуральным, также больше единицы, но имеют не два, а большее количество делителей. Так, например, числа 4, 6, 8, 9 и т. д. являются натуральными, составными, но не простыми числами. Как видите – это в основном четные числа, но не все. А вот “двойка” – четное число и “первый номер” в ряду простых чисел.

Последовательность

Чтобы построить ряд простых чисел, необходимо совершить отбор из всех натуральных чисел с учетом их определения, то есть нужно действовать методом от противного. Необходимо рассмотреть каждое из натуральных положительных чисел на предмет того, имеет ли оно более двух делителей. Давайте постараемся построить ряд (последовательность), который составляют простые числа. Список начинается с двух, следующим идет три, поскольку оно делится только на себя и на единицу. Рассмотрим число четыре. Имеет ли оно делители, кроме четырех и единицы? Да, это число 2. Значит, четыре не является простым числом. Пять также является простым (оно, кроме 1 и 5, ни на какое другое число не делится), а вот шесть – делится. И вообще, если проследить за всеми четными числами, то можно заметить, что кроме “двух”, ни одно из них не является простым. Отсюда сделаем вывод, что четные числа, кроме двух, не являются простыми. Еще одно открытие: все числа, делящиеся на три, кроме самой тройки, будь то четные или нечетные, также не являются простыми (6, 9, 12, 15, 18, 21, 24, 27 и т.д.). То же самое касается и чисел, которые делятся на пять и на семь. Все их множество также не является простым. Давайте подведем итоги. Итак, к простым однозначным числам относятся все нечетные числа, кроме единицы и девятки, а из четных – только “два”. Сами десятки (10, 20. 40 и др.) не являются простыми. Двузначные, трехзначные и т. д. простые числа можно определить, исходя из вышеизложенных принципов: если они не имеют других делителей, кроме их самих и единицы.

Теории о свойствах простых чисел

Существует наука, которая изучает свойства целых чисел, в том числе и простых. Это раздел математики, которая называется высшей. Помимо свойств целых чисел, она также занимается алгебраическими, трансцендентными числами, а также функциями различного происхождения, связанными с арифметикой этих чисел. В этих исследованиях, помимо элементарных и алгебраических методов, также используются аналитические и геометрические. Конкретно изучением простых чисел занимается “Теория чисел”.

Простые числа — “строительные блоки” натуральных чисел

В арифметике есть теорема, которая называется основной. Согласно ей, любое натуральное число, кроме единицы, можно представить в виде произведения, множителями которого являются простые числа, причем порядок следования множителей единственен, этот означает, что и способ представления единственен. Он называется разложением натурального числа на простые множители. Есть и другое название этого процесса – факторизация чисел. Исходя из этого, простые числа можно назвать “строительным материалом”, “блоками” для построения натуральных чисел.

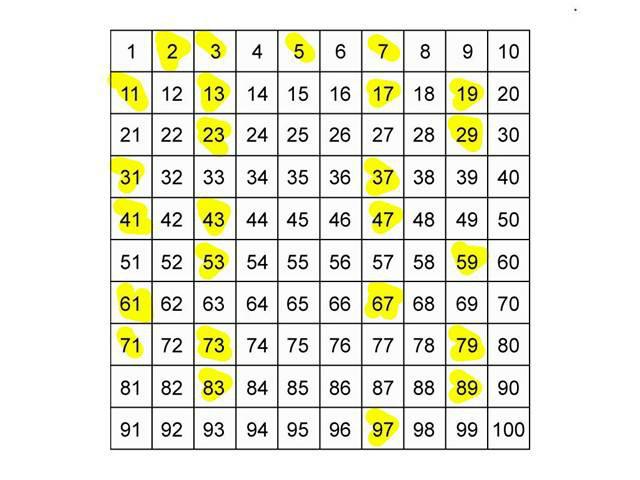
Поиск простых чисел. Тесты простоты

Множество ученых разных времен пытались найти какие-то принципы (системы) для нахождения списка простых чисел. Науке известны системы, которые называются решето Аткина, решето Сундартама, решето Эратосфена. Однако они не дают каких-то существенных результатов, и для нахождения простых чисел используется простая проверка. Также математиками были созданы алгоритмы. Их принято называть тестами простоты. Например, существует тест, разработанный Рабином и Миллером. Его используют криптографы. Также существует тест Каяла-Агравала- Саскены. Однако он, несмотря на достаточную точность, очень сложен в вычислении, что принижает его прикладное значение.

Имеет ли множество простых чисел предел?

О том, что множество простых является бесконечностью, писал в книге “Начала” древнегреческий ученый Евклид. Он говорил так: “Давайте на минуту представим, что простые числа имеют предел. Тогда давайте перемножим их друг с другом, а к произведению прибавим единицу. Число, полученное в результате этих простых действий, не может делиться ни на одно из ряда простых чисел, потому что в остатке всегда будет единица. А это значит, что существует какое-то другое число, которое еще не включено в список простых чисел. Следовательно, наше допущение не верно, и это множество не может иметь предела. Помимо доказательства Евклида, существует более современная формула, данная швейцарским математиком восемнадцатого века Леонардом Эйлером. Согласно ему, сумма, обратная сумме первых n чисел растет неограниченно с ростом числа n. А вот формула теоремы относительно распределения простых чисел: (n) растёт, как n/ln (n).

Какое наибольшее простое число?

Все тот же Леонард Эйлер смог найти самое большое для своего времени простое число. Это 2 31 – 1 = 2147483647. Однако к 2013 году было вычислено другое наиболее точное самое большое в списке простых чисел – 2 57885161 – 1. Его называют числом Мерсенна. Оно содержит около 17 миллионов десятичных цифр. Как видите, число, найденное ученым из восемнадцатого века, в несколько раз меньше этого. Так и должно было быть, ведь Эйлер вел данный подсчет вручную, нашему же современнику наверняка помогала вычислительная машина. Более того, это число было получено на факультете математики в одном из американских факультетов. Числа, названные в честь этого ученого, проходят через тест простоты Люка-Лемера. Однако наука не желает останавливаться на достигнутом. Фонд Электронных рубежей, который был основан в 1990 году в Соединенных Штатах Америки (EFF), назначил за нахождение больших простых чисел денежную награду. И если до 2013 года приз полагался тем ученным, которые найдут их из числа 1 и 10 миллионов десятичных чисел, то сегодня это цифра достигла от 100 миллионов до 1 миллиарда. Размер призов составляет от 150 до 250 тысяч долларов США.

Названия специальных простых чисел

Те числа, которые были найдены благодаря алгоритмам, созданным теми или иными учеными, и прошли тест простоты, называются специальными. Вот некоторые из них:

Простота этих чисел, названных в честь вышеперечисленных ученых, устанавливается с использованием следующих тестов:

4. Биллхарта – Лемера – Селфриджа и др.

Современная наука не останавливается на достигнутом, и, вероятно, в ближайшем будущем мир узнает имена тех, кто смог получить приз в 250.000 долларов, найдя наибольшее простое число.

Источники:

http://urok.1sept.ru/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/592067/
http://zaochnik.com/spravochnik/matematika/delimost/prostye-i-sostavnye-chisla/
http://www.syl.ru/article/144650/mod_kak-nayti-prostyie-chisla