Примеры геометрических фигур в многомерном евклидовом пространстве. Длины и углы

Геометрические фигуры в пространстве

С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельнос­ти (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольни­ков определяют выбор наглядного материала. В этом возрасте важ­но, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсор­ной основе, поэтому с моделями объемных фигур детям знакомить­ся легче. Кубики, шарики, бруски и др. входят в игру детей одно­временно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными фор­мами, а в речь вводятся только некоторые термины.

Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии.

Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.).

Многогранники

Многогранник– это ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Эти многоугольники называются гранями, их стороны — ребрами, а вершины – вершина­ми многогранника.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70).

Выпуклый многогранник невыпуклый многогранник

Задание 43

Покажите вершины, ребра и грани многогранников, изображен­ных на рисунке 70. Какими геометрическими фигурами они явля­ются!

Правильный выпуклый многогранник имеет грани – правильные равные многоугольники, и в каждой его вершине сходится одинако­вое число ребер.

Задание 44

1. Вспомните, какие фигуры называют равными.

2. Назовите известные вам правильные выпуклые многогранники.

Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это об­условлено двумя причинами:

Прямоугольный параллелепипед – это параллелепипед, все грани которого прямоугольники (рис. 75).

Куб — это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76).

Дошкольники, изучая куб, могут отметить, что его поверхность состоит из шести квадратов, что у него 8 вершин. Свойства куба осваиваются ими, например, при выполнении такого задания: «Обклей кубик цветной бумагой. Что для этого нужно?» (вырезать 6 одинаковых квадратов).

Прямоугольный параллелепипед в детском саду часто называют «кирпичиком» или «бруском», что допустимо в предматематической подготовке. Эти слова являются предэталонными названиями гео­метрических фигур, так же как «кубик», «крыша» (треугольная при­зма), «столбик» (цилиндр) и др.

Младшим школьникам можно предложить задание: «Вырежи выкройку для коробки. Какую форму имеет каждая часть?» Таким образом, дети выясняют, что гранями прямоугольного параллелепи­педа являются прямоугольники, не формулируя этого явно.

Пирамида — многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые граны — треугольники.

В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырех­угольные (рис. 776), пятиугольные и другие пирамиды.

Любая грань треугольной пирамиды может служить ее основани­ем. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники.

Форму тетраэдра имеет пакет молока (старой упаковки), а еги­петские пирамиды имеют форму четырехугольной правильной пи­рамиды. Дошкольники называют «пирамидкой» совсем другую мо­дель — игрушку из колец разной величины, которая имеет форму конуса. Эта ситуация может вызвать затруднения в запоминании и правильном применении геометрических терминов у детей. Данная проблема преодолевается при своевременном грамотном объясне­нии и разделении названий игрушек от названий их формы, этало­нами для определения которой служат геометрические фигуры.

Задание 47

1. Нарисуйте пятиугольную пирамиду. Покажите ее основание, бо­ковую поверхность, боковые грани и ребра. Какими геометриче­скими фигурами они являются?

2. Дайте определения высоты пирамиды и правильной пирамиды.

Тела вращения

Изучая форму окружающих предметов, дошкольники сталкива­ются с телами вращения (рис. 78).

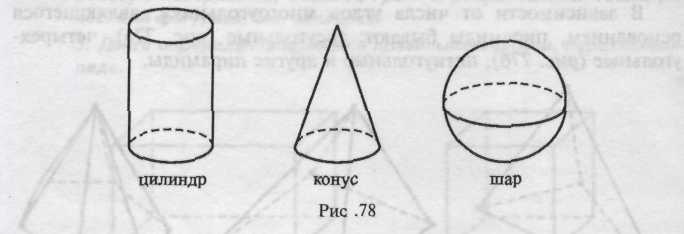
Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур.

Цилиндр – это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси (рис. 79).

Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его кате­тов, как оси (рис. 80),

Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси (рис. 81).

Определения этих фигур из курса геометрии средней школы:

Цилиндр – тело, которое состоит из двух кругов (оснований), совмещаемых параллельным

переносом, и всех отрезков, соединяющих

соответствующие точки этих кругов.

Конус – тело, которое состоит из круга (основания), точки (вер­шины), не лежащей в плоскости этого круга, и всех отрезков, сое­диняющих вершину конуса с точками основания.

Шар— тело, которое состоит из всех точек пространства, нахо­дящихся на расстоянии не более заданного (радиуса) от данной точ­ки (центра).

Задание 48

— высоты цилиндре и прямого цилиндра;

— образующей конуса, высоты конуса и прямого конуса.

Дошкольники не знакомятся с этими формулировками, но мо­гут различать и узнавать объемные тела, а если провести спе­циальную работу, и правильно называть их. Дети усваивают свой­ства этих фигур в сравнении с другими. Например, во время игры «Катится — не катится» они выясняют, что: «Цилиндр, стоящий на основании, устойчив, как куб, но если его положить – катится, как шар».

Обследование поверхности дает знание того, что основанием цилиндра и конуса является круг. Рисование объемных предметов разной формы на плоскости учит детей сравнивать, проводить ана­логию, моделировать, трансформировать пространство на плоскос­ти. Например, в процессе обсуждения таких вопросов: «Какой фор­мы мяч? Какую фигуру надо нарисовать, чтобы изобразить мяч?»

Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, раз­вивает мышление.

Вопросы для самоконтроля к теме № 3

1. Что изучает геометрия?

2. Что изучает планиметрия?

3. Что изучает стереометрия?

4. Что называется геометрической фигурой?

5. Назовите правила построения геометрии.

6. Назовите основные фигуры на плоскости и в пространстве.

7. Какие фигуры называются плоскими?

8. Какие фигуры называются выпуклыми?

9. Дайте определение отрезка.

10. Дайте определение луча.

11. Дайте определение угла.

12. Какая линия называется ломаной?

13. Какая ломаная называется простой?

14. Дайте определение многоугольника.

15. Какой многоугольник называется выпуклым?

16. Какой многоугольник называется правильным?

17. Дайте определение треугольника.

18. Какой треугольник называется равносторонним, какой — равно­бедренным, какой – разносторонним?

ТЕМА 4

ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ

Понятие величины

Величина – одно из основных математических понятий, воз­никшее в древности и в процессе длительного развития подвергшее­ся ряду обобщений. Длина, площадь, объем, масса, скорость – это величины.

Задание 49

Приведите примеры различных величии, изучаемых в школе на уроках математики, физики, химии. Вспомните способы их изме­рения и единицы этих величин.

Величины представляют собой особые свойства реальных пред­метов или явлений, которые проявляются при сравнении их по это­му свойству, причем каждая величина связана с определенным спо­собом сравнения. Например, длину отрезков можно сравнить спо­собом наложения, а массу предметов – взвешиванием. Величины можно оценивать количественно на основе сравнения.

Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свойства конкрет­ного объекта. Например, свойство предметов «иметь протяжен­ность» называется «длиной».

Однородные величины – величины, которые выражают одно и то же свойство объектов некоторого класса. Например, длина, шири­на, периметр — однородные величины.

Разнородные величины выражают различные свойства объектов (один предмет может иметь массу, объем и др.).

Геометрия k-плоскостей в аффинном и евклидовом пространствах

Пусть в n-мерном аффинном пространстве U_n зафиксирована произвольная точка А, и в соответствующем линейном пространстве L_n зафиксировано произвольное k-мерное подпространство L_k.

Определение. Множество всех точек М аффинного пространства, для которых АМ L_k, называют k-мерной плоскостью, проходящей через точку А в направлении подпространством L_k.

Рис. 11, где k = 2

Говорят также, что L_k есть направляющее подпространство этой плоскости. Очевидно, что каждая плоскость определяет однозначно своё направляющее пространство.

Точку М называют текущей точкой плоскости. На рисунке показаны три положения М₁, М₂, М₃ текущей точки М.

Частные случаи k-плоскостей

Если k = 0, то плоскость состоит из одной точки А. Поэтому каждую точку аффинного пространства можно рассматривать как нуль-мерную плоскость.

Одномерная плоскость называется прямой линией.

Плоскость размерности n – 1 называется гиперплоскостью.

При k = n плоскость совпадает со всем пространством U_n.

В определении плоскости выделена точка А. Докажем, что в действительности все точки плоскости равноправны.

Обозначим плоскость через П_k и зафиксируем произвольную точку В . Надо доказать, что точка М принадлежит плоскости П_k тогда и только тогда, когда (т. е. что любая точка М может играть роль А).

Пусть . По определению плоскости . Отсюда и по определению подпространства , поэтому . Обратно, если , то следовательно, .

Теорема. Всякая k-мерная плоскость в аффинном пространстве сама является k-мерным аффинным пространством.

Доказательство. Пусть дано аффинное пространство U, которому соответствует линейное пространство L, пусть П_k – плоскость, проходящая через точку А в направлении подпространства L_k. Возьмём в плоскости П_k две произвольные точки M, N . По определению аффинного пространства им соответствует вектор . По определению плоскости векторы АМ и АN принадлежат подпространству L_k.

Следовательно, . Таким образом, каждой упорядоченной паре точек М, N плоскости П_k, поставим в соответствие вектор MN из k-мерного пространства L_k. При этом соблюдаются для П_k аксиомы, вытекающие из определения k-мерной плоскости и для всего аффинного пространства U. Теорема доказана.

Замечание. Если плоскость проходит через начало аффинной системы координат в направлении подпространства L_k, то совокупность радиус-векторов её точек образует подпространство, по определению совпадающее с подпространством L_k.

Пусть в аффинном пространстве U даны точки А, А₁,…, А_k (в числе k + 1). Эти точки находятся в общем положении, если они не принадлежат ни одной (k -1)-мерной плоскости .

Проверим, что точки А, А₁,…, А_k находятся в общем положении тогда и только тогда, когда векторы АА₁,…, АА_k линейно независимы (рис. 13), причём безразлично, какую из точек брать в качестве А (то есть за начало векторов, идущих из неё в другие точки).

Из сказанного в этом пункте и из определения плоскости следует, что через систему точек А, А₁,…, А_k, находящихся в общем положении, проходит k-мерная плоскость и притом только одна.

Предположим, что в пространстве U_n зафиксирована какая-нибудь аффинная система координат с началом О и базисом е₁, е₂, …, е_n. Рассмотрим плоскость П_k, проходящую через точку А в направлении подпространства L_k.

Будем считать, что точка А имеет координаты р₁, р₂, …, р_n и что L_k задаётся как независимая система векторов q₁, q₂, …, q_k. Тогда радиус-вектор ОМ текущей точки плоскости можно записать в виде

где параметры ф1, ф2, …, фk независимо друг от друга пробегают всевозможные числовые значения, а вектор (рис. 14)

Координаты текущей точки М обозначим, как обычно, через (x₁, x₂, …, x_n) и запишем векторное равенство в координатах. В результате получим n числовых равенств.

Эти равенства называются параметрическими уравнениями плоскости П_k.

Пример. Пространство, изучаемое в стереометрии, является трёхмерным аффинным пространством. В нём одномерные и двумерные плоскости совпадают соответственно с прямыми линиями и плоскостями, понимаемыми в элементарно-геометрическом смысле. В отличие от пространства, изучаемого в элементарной геометрии, в аффинном пространстве не определены метрические понятия: расстояния между точками и длины линий, площади и объёмы фигур, углы и перпендикулярность. При исследовании фигур в аффинном пространстве изучаются лишь те геометрические свойства, которые не зависят от метрических понятий.

2. Уравнения k-плоскости по k+1 точкам

Если заданы k+1 точек А(х), А₁(х₁), …, А_n(х_n) и векторы АА_{а =} х_а – х независимы, то эти точки определяют единственную k – плоскость, проходящую через них: в этом случае за направляющие векторы этой плоскости можно принять векторы АА_а и векторное уравнение k-плоскости можно записать в виде

В дальнейшем будем часто иметь дело с k-поверхностями и k-плоскостями при k = n – 1. Говоря, «поверхность n-пространства» и «плоскость n-пространства», но иметь в виду (n – 1)-поверхность и (n – 1)-плоскость этого пространства. Часто поверхность и плоскость называется соответственно гиперповерхностью и гиперплоскостью.

Поверхность можно задать одним координатным уравнением

если координаты x i , удовлетворяющие этому уравнению, можно представить как функции n – 1 параметров t₁, t₂, …, t_n-1, то получим

3. Взаимное расположение плоскостей

3. 1 Пересекающиеся плоскости

Во всём этом пункте размерности плоскостей и подпространств обозначены индексами снизу. Пусть две плоскости П_k и П_l пересекаются, то их пересечением является некоторая плоскость П_m.

Замечание 1. Не исключена возможность, что П_m состоит из одной точки (m = 0). Это видно на примере двух пересекающихся прямых или прямой и плоскости (рис. 16).

В общем случае по одной точке могут пересекаться две плоскости, сумма разностей которых не превышает размерности пространства, например, двумерные плоскости в четырёхмерном пространстве.

Замечание 2. Не исключено и другое, когда одна из двух плоскостей целиком принадлежит другой. Например, , тогда (рис. 17)

2) Если плоскости П_k и П_l пересекаются по плоскости П_m, то существует единственная плоскость П_r, размерности r = k + l – m, содержащая П_k и П_l, причём ни в какой плоскости меньшей размерности П_k и П_l не могут одновременно поместиться. Направляющее подпространство L_r плоскости П_r является суммой направляющих подпространств L_k и L_l. Эта сумма является прямой суммой тогда и только тогда, когда П_k и П_l пересекаются по одной точке (m = 0, см. рис. 18).

В частном случае, когда n = k + l – m, роль плоскости П_r выполняет всё пространство U_n (при r = n = 3 см. рис. 15).

3) Если пересекающиеся плоскости П_k и П_l содержатся в какой-нибудь плоскости П_r, то размерность их пересечения . В частности, для любых двух непересекающихся плоскостей из U_n.

4) Если плоскости П_k и П_l проходят через точку А в направлении подпространств L_k и L_l соответственно и если L_k содержится в L_l, то плоскость П_k содержится в плоскости П_l. Если при этом k = l, то П_k совпадает с П_l (также и L_k совпадает с L_l).

Пусть теперь плоскость П_k определяется точкой А и подпространством L_k, а плоскость П_l – точкой В и подпространством L_l. Будем считать, что .

Определение: Плоскость П_k параллельна плоскости П_l, если .

В этом случае плоскость П_l параллельна плоскости П_k.

Замечание 1. Согласно этому определению включение является частным случаем параллельности.

Замечание 3. Убедимся, что при n = 3 частные случаи k = l = 1,

k = l = 2 и k =1, l = 2 согласуются с понятием параллельности прямых и плоскостей, известным из элементарной геометрии (рис. 19)

Пусть в произвольной аффинной системе координат две плоскости П и П l одинаковой размерности заданы системами линейных уравнений. Пользуясь определением параллельности, нетрудно установить следующее утверждение.

Утверждение. Для того, чтобы П и П‘ были параллельными, необходимо и достаточно, чтобы соответствующие однородные системы уравнений были эквивалентны.

В частности, две гиперплоскости параллельны тогда и только тогда, когда в одних и тех же координатах они задаются уравнениями

с пропорциональными коэффициентами при переменных:

Теорема 1. Пусть в аффинном пространстве U_n даны плоскость П_k и точка В. Тогда существует единственная плоскость размерности k, проходящая через точку В параллельно П_k. Если , то совпадает с П_k; если точка В расположена вне П_k, то плоскости П_k и не пересекаются.

Определение. Две плоскости называются скрещивающимися, если они не пересекаются и не параллельны.

Известно, что в трёхмерном пространстве U₃ две прямые линии, т. е. одномерные плоскости, могут скрещиваться, тогда как прямая линия и двумерная плоскость в U₃ скрещиваться не могут. С повышением размерности пространства оно становится более просторным, в результате чего появляется возможность строить в нём скрещивающиеся плоскости разных размерностей, а не только одномерные. Ниже сформулирована теорема 2, содержание которой можно рассматривать как общий приём построения скрещивающихся плоскостей. Именно, пусть в аффинном пространстве U_n дана плоскость П_l (l

Выпуклые многогранники с паркетными гранями в многомерных евклидовых пространствах Текст научной статьи по специальности «Математика»

Аннотация научной статьи по математике, автор научной работы — Гурин Алексей Михайлович, Архаров Денис Владимирович, Петров Леонид Викторович, Попов Алексей Николаевич, Черный Александр Семенович

Статья состоит из трех разделов. В первом разделе дан краткий обзор исследования выпуклых многогранников с правильными гранями, расположенными в трехмерном евклидовом пространстве. Во втором разделе поставлены новые задачи, в том числе о доказательстве существования паркетных граней у выпуклых многогранников с правильными гранями. В третьем разделе доказана новая теорема о многогранниках с паркетными гранями в четырехмерном евклидовом пространстве.

Похожие темы научных работ по математике , автор научной работы — Гурин Алексей Михайлович, Архаров Денис Владимирович, Петров Леонид Викторович, Попов Алексей Николаевич, Черный Александр Семенович

CONVEX POLYHEDRA WITH PARQUET FACES IN MULTIDIMENSIONAL EUCLIDEAN SPACES

The paper consists of three sections. The first section provides a brief overview of the study of convex polyhedra with regular faces, arranged in threedimensional Euclidean space. The second section presents new tasks, such as, in particular, proving the existence of parquet faces in convex polyhedra with regular faces. The third section proves a new theorem on polyhedra with parquet faces in four-dimensional Euclidean space.

Текст научной работы на тему «Выпуклые многогранники с паркетными гранями в многомерных евклидовых пространствах»

ВЫПУКЛЫЕ МНОГОГРАННИКИ С ПАРКЕТНЫМИ ГРАНЯМИ В МНОГОМЕРНЫХ ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ

CONVEX POLYHEDRA WITH PARQUET FACES IN MULTIDIMENSIONAL EUCLIDEAN SPACES

A.M. Гурин, Д.В. Архаров, /1.В. Петров, А.М. Gurin, D.V. Arkharov, L.V. Petrov, A.N. Popov,

A.H. Попов, A.C. Черный A.S. Cherny

Многогранники, ребра, разбиение пространства, паркетные грани, гиперграни.

Статья состоит из трех разделов. В первом разделе дан краткий обзор исследования выпуклых многогранников с правильными гранями, расположенными в трехмерном евклидовом пространстве. Во втором разделе поставлены новые задачи, в том числе о доказательстве существования паркетных граней у выпуклых многогранников с правильными гранями. В третьем разделе доказана новая теорема о многогранниках с паркетными гранями в четырехмерном евклидовом пространстве.

Polyhedra, ribs, space partitioning, hardwood faces, facets.

The paper consists of three sections. The first section provides a brief overview of the study of convex polyhedra with regular faces, arranged in three-dimensional Euclidean space, The second section presents new tasks, such as, in particular, proving the existence of parquet faces in convex polyhedra with regular faces. The third section proves a new theorem on polyhedra with parquet faces in four-dimensional Euclidean space.

Настоящая статья пополняет список работ, расширяющих исследования выпуклых многогранников трехмерного евклидова пространства [Александров, 2007] на аналогичные многогранники в многомерных пространствах. Здесь обобщается задача Пряхина [Пря-хин, 1974] об изучении выпуклых многогранников с паркетными гранями в трехмерном евклидовом пространстве. Напомним определения Пряхина [Пряхин, 1974, с. 111].

Определение 1. Выпуклый многоугольник называется равноугольным, если все его углы равны между собой.

Определение 2. Выпуклый многоугольник называется паркетным, если он может быть составлен из конечного числа равноугольных многоугольников.

В приведенных определениях по умолчанию допускается, что многоугольники могут быть подклеены друг к другу не только по целой грани, говорят, нормальным образом, но и по части грани. Об этом допущении можно точно узнать из соответствующей таблицы типов паркетных граней [Там же], где приведены соответствующие типы паркетных граней. Список типов паркетных граней

станет короче, если оставим из списка паркетных граней лишь те грани, что получены подклейкой составляющих их многоугольников по целым ребрам.

Определение 3. Нормальной паркетной гранью называется выпуклый многоугольник, составленный из правильных выпуклых многоугольников при помощи подклейки друг к другу правильных многоугольников по целым ребрам.

Рассмотрим ряд примеров. Два отдельно взятых правильных треугольника можно расположить в одной плоскости и подклеить друг к другу по целому ребру или по части ребра. Если подклеим по части ребра, то условие выпуклости не выполнится. Если подклеим по целому ребру, то полученное соединение треугольников, граница которого известна как ромб, в рассматриваемом классе многоугольников суть пример паркетного многоугольника или грани.

Продолжим построение паркетных граней в рамках определения 3. Подклеим к паре треугольников еще один правильный треугольник. Подклейку можно осуществить лишь единственным способом. Получим паркетную грань, выпуклая оболочка которой суть трапеция. Паркетная грань

А.М. ГУРИН, Д.В. АРХАРОВ, Л.В. ПЕТРОВ, А.Н. ПОПОВ, А.С. ЧЕРНЫЙ. ВЫПУКЛЫЕ МНОГОГРАННИКИ С ПАРКЕТНЫМИ ГРАНЯМИ

В МНОГОМЕРНЫХ ЕВКЛИДОВЫХ ПРОСТРАНСТВАХ

имеет условную вершину, которая лежит внутри ребра основания трапеции.

Подклейка четвертого треугольника к паркетной грани в составе трех треугольников возможна ровно тремя независимыми способами, так как ровно три различных ребра имеет трапеция. Подклейка к верхнему основанию трапеции дает в целом треугольник с тремя условными вершинами. Подклейка к боковому ребру трапеции дает в целом параллелограмм с двумя условными вершинами. Подклейка к основанию трапеции в условиях определения 3 дает невыпуклый многоугольник. Заметим, что в условиях определения 2 подклеить можно треугольник по всему основанию трапеции и получим один из паркетных многоугольников Пряхина. В нем образуется одна условная вершина внутри многоугольника.

Аналогично, оставаясь в условиях определения 3, получим условную вершину внутри шестиугольника, образованного шестью правильными треугольниками с общей вершиной.

Если рассматривать нормальные паркетные грани без условных вершин, то из списка числа типов граней Пряхина останутся только пять граней, составленных из двух или трех правильных граней. Выпуклые многогранники с гранями без условных вершин были найдены в работах [Johnson 1966; Залгаллер, 1967; Иванов, 1971; Пряхин, 1973; Турин, Залгаллер, 2008; Тимофеенко, 2008; 2011].

При переходе к паркетным граням с условными вершинами появляется необходимость детального пояснения предмета исследования, начиная с определения. Обратимся к примеру шестиугольной грани, для которой проявляется свойство быть правильной гранью в классе правильных граней и быть паркетной в классе паркетных граней. Свойством шестиугольной грани обладают еще две правильные грани, которые также входят в список паркетных граней Пряхина [Александров, 2007]. Аналогично, обратившись к многогранникам с правильными гранями, можно указать многогранники, составленные, в свою очередь, из иных многогранников с правильными гранями. Залгаллер разделил многогранники на простые многогранники и составленные из простых многогранников [Залгаллер, 1967]. Составленные получались при помощи операции подклеивания простых многогранников по целым граням друг к

другу, но лишь так, что найдется плоскость, разбивающая составленный многогранник на два многогранника с правильными гранями. Определение простого многогранника, по Залгаллеру, говорит, что для него не существует плоскости, способной рассечь его на два многогранника с правильными гранями, если плоскость проходит по ребрам многогранника.

Если все вершины многогранника трехгранные, то он тоже простой, так как его нельзя разбить плоскостью на два многогранника, если плоскость проходит по одним лишь ребрам.

Это определение было включено в алгоритм нахождения перечня простых многогранников Залгаллера, а составные многогранники были получены прикладыванием простых многогранников друг к другу по целым граням [Залгаллер, 1967]. Оказалось, что таким путем получаются все многогранники Джонсона роИпБоп, 1966]. Это показано в статье [Залгаллер, 1967]. В работах [Турин, Залгаллер, 2008; Тимофеенко, 2008; 2011] показано, что иных многогранников нет, если грани суть правильные многоугольники. Там же завершено перечисление многогранников с паркетными гранями, если грани не имеют условных вершин.

В многомерном пространстве, начиная от разбиения трехмерного евклидова пространства на выпуклые многогранники с правильными гранями, исследования начаты в работе [Турин, Залгаллер, 2008]. Здесь приводится пример существования нормальных паркетных граней в смысле определения 3 для четырехмерного и пятимерного евклидова пространства.

Теорема. Четырехмерный куб представим как совокупность пирамид с правильными двумерными гранями над трехмерными кубами.

Доказательство теоремы выполняется по схеме:доказывается существование пирамиды с правильными двумерными гранями в четырехмерном евклидовом пространстве;

доказывается, что пирамида над гиперкубом в пятимерном пространстве вырожденная, то есть вершина пирамиды лежит в плоскости гиперкуба, а четырехмерные пирамиды над трехмерными кубами разбивают четырехмерный гиперкуб, подобно тому как правильные треугольники разбивают шестиугольник на двумерной плоскости.

Применяя паркетное разбиение гиперкуба легко, находим перечень пятимерных кубов с паркетными гипергранями гиперкуба.

1. Александров А.Д. Выпуклые многогранники // Избранные труды. Новосибирск: Наука, 2007. Т. 2. 457 с.

2. Турин А.М., Залгаллер В.А. К истории изучения выпуклых многогранников с правильными гранями и гранями, составленными из правильных // Труды Санкт-Петербургского математического общества. 2008. Декаб. Т. 14. С. 215-292.

3. Залгаллер В.А. Выпуклые многогранники с правильными гранями // Записки научных семинаров ЛОМИ. 1967. Т. 2. С. 1-220.

4. Иванов Б.И. Многогранники с гранями, сложенными из правильных многоугольников // Украинский геометр, сб., 1971. Вып. 10. С. 20-34.

5. Пряхин Ю.А. Выпуклые многогранники, грани которых равноугольны или сложены из равноугольных // Записки научных семинаров ЛОМИ. 1974. Т. 45. С. 111-112.

6. Пряхин Ю.А. О выпуклых многогранниках с правильными гранями // Украинский геометр, сб., 1973. Вып. 14. С. 83-88.

7. Тимофеенко А.В. Выпуклые правильногран-ники, не рассекаемые никакой плоскостью на правильногранные части // Матем. тр. 2008. Т. 11. № 1. С. 132-152.

8. Тимофеенко А.В. О выпуклых многоран-никах с равноугольными и паркетными гранями // Чебышевский сборник. 12. 2011. Вып. 2. С. 118-126.

Источники:

http://lektsii.org/10-96516.html
http://studbooks.net/2300896/matematika_himiya_fizika/geometriya_ploskostey_affinnom_evklidovom_prostranstvah
http://cyberleninka.ru/article/n/14749508