Парадокс дихотомии. Апории зенона о движении

Парадоксы Зенона Элейского – описание, значение и интересные факты

Парадоксы Зенона вводили в недоумение многих ученых и философов до 17 века. И до сих пор многие ученые спорят о бесконечности, структуре пространства и времени, хотя началось все с нескольких парадоксальных утверждений, ставящих поначалу в логический тупик любого умного человека.

История возникновения парадоксов Зенона

Зенон Элейский – философ Древней Эллады, ученик основателя Элейской школы – Парменида. Жил он с 515 по 450 год до нашей эры, о его жизни известно очень мало. Родился в городе Элее в южной части Италии. По утверждению Платона, Зенон побывал в Афинах и встретился с Сократом. Прославился благодаря своим апориям, в виде которых был сформулирован знаменитый парадокс Зенона. Апории Зенона представляют собой парадоксальные рассуждения, само же слово «апория» с греческого языка обозначает «безвыходность».

В древние времена современники насчитывали 40 парадоксальных утверждений, а до наших дней дошли только 9, наиболее известны – 4. Узнали об апориях Зенона благодаря трудам Аристотеля, а также благодаря таким философам, как Диоген Лаэртский, Платон, Филопон, Симпликий. Кстати, стоит сказать о самой Элейской школе, к которой Зенон принадлежал. Основные ее учения гласят, что любое изменение является иллюзией, бытие же является единым и не изменяется. Зенон говорил, что истинная реальность является вечной и неизменной, и постигнуть ее можно только с помощью разума и логики. Поэтому многие апории Зенона посвящены движению, в них он показывает, что движения (или изменения), с точки зрения логики, не существует.

Парадоксы о движении и времени

«Состязание Ахиллеса и черепахи» – один из самых известных парадоксов Зенона. Наверное, его знает каждый школьник. Существуют еще такие апории Зенона, как «Полет стрелы», «Дихотомия» и другие. Они посвящены движению, обсуждаемы и изучаются уже два тысячелетия. Им посвящены были многие исследования, и вплоть до 17 века мыслители не могли опровергнуть эту хитроумную логику.

Проблема решилась после идеи дифференциального исчисления, которую предложили Ньютон и Лейбниц. Там есть понятие «предел», так прояснилась разница между разбиением времени и разбиением на отрезки определенного пути. К тому же загадка разрешилась, когда ученые научились пользоваться бесконечно малыми величинами. Апории Зенона породили с тех пор множество различных вариаций. Кроме того, возможно, добавились некоторые детали. Мы перечислим сохранившиеся до наших дней парадоксы Зенона и кратко расскажем об их сути. Во всяком случае, попытаемся это сделать.

Парадокс Зенона об Ахиллесе и черепахе

Герой мифов Древней Греции Ахиллес соревнуется в скорости бега с черепахой. Условия таковы, что черепаха стартует немного дальше, Ахиллес находится от нее на расстоянии в 1000 шагов.

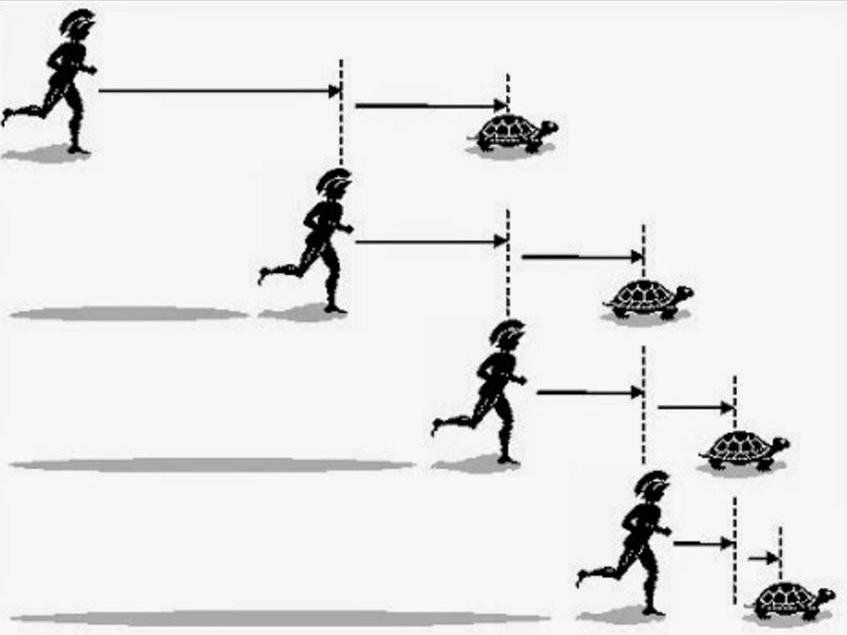
Чтобы догнать черепаху, Ахиллес должен достигнуть сначала места, с которого черепаха стартовала. Но как только он добежит до этого места, черепаха успеет проползти 100 шагов. Это расстояние, которое она проползла, еще предстоит преодолеть Ахиллесу, но к тому времени она уползет еще дальше на 10 шагов и так далее. Число таких отрезков, которые нужно преодолеть Ахиллесу, по утверждению Зенона, может быть бесконечным, ведь величина этих отрезков все время будет уменьшаться до бесконечно малых величин.

Выходит, если следовать такой логике, древнегреческий герой никогда не догонит черепаху. Парадокс Зенона заключается в существовании бесконечного количества бесконечно малых отрезков, но в реальной жизни бегун наверняка обгонит медлительное животное.

Летящая стрела

Этот парадокс получил название «Стрела». Это еще одна апория, которую Зенон сформулировал приблизительно следующими словами. Если что-либо пребывает в движении, то оно движется либо в том месте, которое оно занимает собой, либо оно движется там, где его нет. Но оно не способно двигаться в том месте, которое оно занимает. Так как в каждую секунду оно занимает полностью все это место. Но и в том месте, где его нет, оно не может двигаться. Следовательно, движение само по себе невозможно.

По утверждению Зенона, стрела, когда летит, одновременно пребывает в покое. Потому что в каждый момент она занимает одно и то же пространство, равное ей. То есть стрела пребывает в покое относительно места, где она находится в определенный промежуток времени. Получается, что летящая стрела неподвижна. Если она неподвижна в определенный момент, значит, она находится в покое и в другие моменты времени. И нет того момента, когда стрела двигалась.

Дихотомия

Парадокс, который будет приведен далее, имеет название «дихотомия». В переводе с греческого языка оно означает «разделение надвое», и дано оно Аристотелем. Эта апория изложена примерно по такому же принципу, как и парадокс Зенона об Ахиллесе и черепахе.

В оригинале говорится о бегуне, который не в состоянии даже стартовать, ведь движения, по мнению Зенона, не существует. Но есть еще и распространенный вариант про пересечение комнаты.

Чтобы пересечь комнату, нужно сначала пересечь половину комнаты. На это уйдет определенная единица времени. После этого останется определенное расстояние, нужно преодолеть половину его за еще одну единицу времени. Затем тот отрезок пути, что остался, нужно разделить еще надвое и пройти половину этого отрезка за то же время. Тогда опять остается определенное расстояние, половину которого надо пересечь. Получается, что комнату пересекать можно бесконечно.

Две колонны на стадионе

Две колонны людей, одинаковые по длине, двигаются параллельно с одинаковой скоростью в противоположных направлениях. По утверждению Зенона, время которое истечет, когда колонны будут проходить мимо друг друга, равно половине того времени, которое нужно одному человеку, чтобы пройти мимо всей колонны.

Разрешение парадоксов Зенона

Из четырех перечисленных апорий наибольшую известность получили первые три. Четвертая появилась из-за неправильного понимания природы относительного движения.

Все апории можно легко опровергнуть экспериментально. Ничего не мешает пересечь комнату, выпустить стрелу и обогнать черепаху.

Рассмотрим парадокс, связанный с пересечением комнаты. Конечно, если разделить расстояние надвое и пройти половину, на это уйдет определенное количество времени. Останется еще расстояние, которое тоже нужно поделить надвое и пройти половину. Но для этого времени понадобится в два раза меньше. Чем меньше становится расстояние, которое необходимо преодолеть, тем больше будет сокращаться время на его прохождение. Выходит, при пересечении комнаты в конце требуется неограниченное число бесконечно маленьких временных отрезков. Но если сложить все отрезки, получится определенное число – оно-то и будет временем, затраченным на пересечение комнаты. Получается, пересечь комнату вполне возможно за определенный промежуток времени. Это доказательство схоже с нахождением предела при дифференциальном исчислении. Древнегреческий философ Зенон ошибочно предполагал, что при прохождении бесконечно малых расстояний каждый раз требуется одно и то же время.

Что касается парадокса Зенона «Летящая стрела», еще Аристотель его раскритиковал, утверждая, что каждый момент времени не может быть неделимым сам по себе. Еще он говорил, что рассуждения Зенона о том, что если все занимающее равное себе место пребывает в покое, и если то, что пребывает в движении, всегда занимает в любой момент такое же место, то стрела неподвижна, ошибочны.

Квантовый эффект

Парадоксы Зенона были опровергнуты со временем многими учеными. Но они все же внесли определенный вклад в науку. В квантовой физике на сегодняшний момент есть такое понятие, как квантовый парадокс Зенона. Он заключается в том, что если наблюдать за нестабильной частицей, например, проводить измерения, проверять, распалась частица или нет, то возникает некоторое замедление радиоактивного распада.

Предполагается, что если непрерывно наблюдать за частицей, то она может вообще не распасться. В 90-х годах прошлого века этот квантовый эффект был подтвержден с помощью ряда экспериментов.

15 парадоксов, которые взорвут ваш мозг

Я знаю, что ничего не знаю. Так сказал однажды Сократ.

Это заявление само по себе парадоксально, потому как демонстрирует сложность значения одного слова.

Также оно объясняет понимание видения мира одним из основателей западной философии: вы должны подвергать сомнению всё, что вы думаете, что знаете.

Действительно, чем глубже копать, тем больше парадоксов вокруг вы начнёте видеть.

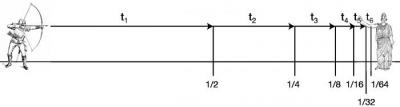
1. Чтобы дойти куда-либо, вы должны сначала пройти полпути, затем пройти половину из оставшейся половины, потом ещё половину оставшегося расстояния и так до бесконечности: таким образом, движение невозможно.

Парадокс дихотомии считается детищем древнегреческого философа Зенона, который якобы был создан для доказательства того, что Вселенная уникальна и что любое изменение, включая движение, невозможно (такого же мнения придерживался и его учитель Парменид).

Люди интуитивно отвергают этот парадокс на протяжении уже многих лет.

С математической точки зрения решение, к которому пришли ещё в 19 веке, состоит в том, чтобы принять, что половина плюс одна четверть плюс одна восьмая плюс одна шестнадцатая и так далее вплоть до одного. Это похоже на число 0,999…., которое когда-то станет 1.

Но данное теоретическое решение на самом деле не объясняет, как именно объект достигает пункта назначения. Решение этого вопроса более сложное и до сих пор не ясное, учитывая теории 20 века о материи, времени и пространстве, которые неделимы.

2. В любой момент движущийся объект неотличим от неподвижного, поэтому движение невозможно.

Это парадокс называется парадоксом стрелы, и это ещё один аргумент Зенона против движения. Проблема здесь в том, что в один момент времени проходит 0 секунд, и поэтому движение в данном случае нулевое.

Зенон утверждал, что если бы время было составлено из мгновений, то тот факт, что движение не происходит в какой-то конкретный момент, говорил бы о том, что оно не происходит вообще.

Как и парадокс дихотомии, парадокс стрелы фактически намекает на современные представления о квантовой механики. В книге “Размышления об относительности” (“Reflections of Relativity”) Кевин Браун отмечает, что в контексте специальной теории относительности объект в движении отличается от неподвижного объекта.

Относительность требует, чтобы объекты, движущиеся с различной скоростью, по-разному представлялись стороннему наблюдателю, а также, чтобы они сами по себе имели различные преставления об окружающем мире.

Интересные парадоксы

3. Если вы восстановили корабль, заменив все его деревянные части, это остался тот же корабль?

Ещё один классический парадокс из Древней Греции, “Корабль Тесея” – это парадокс о противоречиях идентичности. Его хорошо описал Плутарх.

Корабль, на котором Тесей и молодёжь Афин возвращались с Крита, имел 30 весёл, которые были сохранены вплоть до времён Димитрия Фалерея. А всё благодаря тому, что когда старые деревянные доски начали разлагаться, их заменили на новые, более крепкие.

Они держались так долго, что этот корабль стал постоянной темой обсуждения среди философов, которые говорили о логике разных вещей, которые изменяются. Одна группа философов говорила, что корабль остался тем же, в то время, как другие философы настаивали, что после замены брёвен, корабль стал другим.

4. Может ли Всемогущий создать скалу, слишком тяжёлую для того, чтобы он сам мог её поднять?

Как может существовать зло, если Бог всемогущ? Как можем мы называть себя свободными, если Бог всеведущ?

Это лишь несколько из многих существующих парадоксов, касающихся применения вопросов логики к божественной теме.

Некоторые люди могут ссылаться на эти парадоксы, объясняя тем самым, почему они не верят в высшее существо. Однако, другие говорят, что они несущественны и по разным причинам не работают.

Удивительные парадоксы

5. Существует бесконечно длинный “рог”, которые имеет конечный объём, но бесконечную площадь поверхности.

Двигаясь навстречу проблеме, появившейся в 17 веке, мы получаем один из многих парадоксов, связанных с геометрией и бесконечностью.

“Рог Гавриила” формируется путём взятия кривой y = 1/х и поворота вокруг горизонтальной оси, как показано на рисунке.

Используя методы исчисления, которые позволяют вычислить площади и объёмы построенных таким образом фигур, можно видеть, что бесконечно длинный рог фактически имеет конечный объём, равный числу пи, но бесконечную площадь поверхности.

Иными словами, в рог поместится определённое количество краски, но для того, чтобы покрыть краской всю его поверхность, потребуется её бесконечное количество.

6. Гетерологическое слово – это слово, которое не описывает себя. А описывает ли себя слово “гетерологический”?

Это один из многих парадоксов, который долго томил умы современных математиков и логиков.

Примером гетерологического слова может быть слово “глагол”, которое не является глаголом по сути (в отличие от “существительного”, которое является существительным). Другим примером может быть слово “длинный”, которое не является длинным словом (в отличие от слова “короткий”, которое является коротким словом).

Так “гетерологический” является гетеролигическим словом или нет? Если бы это было бы слово, которое не описывает себя, тогда оно бы описывало себя. А если бы оно было словом, которое описывает себя, оно бы не описывало себя.

Это связано с парадоксом Рассела, который спрашивает, содержит ли определённое множество себя в качестве элемента.

Создавая подобные самоуничтожающиеся множества, Бертран Рассел (Bertrand Russell) и другие учёные продемонстрировали важность установления тщательных правил при создании множеств, которые заложили основу математики 20 века.

Самые невероятные парадоксы

7. Пилоты могут “выйти” из боевого режима, если они психологически непригодны, но каждый, кто хочет “выйти” из боевого дежурства, доказывает, что он нормален.

“Уловка -22” – это сатирический роман о Второй мировой войне Джозефа Хеллера (Joseph Heller), в котором описывается ситуация, когда кто-то нуждается в чём-то, что можно получить только тогда, когда он в этом не нуждается.

Это так называемый парадокс саморефенеции. Главный герой романа Йоссариан столкнулся с этим парадоксом при оценке пилотной деятельности, но в итоге, куда бы он направлялся, он везде видел парадоксальные и репрессивные правила.

8. В каждой цифре есть что-то интересное.

1 – это первое ненулевое натуральное число, 2 – наименьшее простое число, 3 – первое нечётное простое число, 4 – наименьшее составное число и т.д. Когда вы наконец доберетесь до числа, которое покажется вам неинтересным, то это число окажется интересным из-за того, что оно показалось вам неинтересным.

Парадокс интересного числа основан на неточном определении слова “интересный”, что делает его несколько более глупым вариантом гетерологического парадокса и парадокса Рассела, которые полагаются на противоречивые самореференции.

Исследователь квантовых вычислений Натаниэль Джонстон (Nathaniel Johnston) нашёл умное решение парадокса. Вместо того, чтобы полагаться на интуитивное понятие слова “интересно”, как в исходном парадоксе, он определил интересное целое число как таковое, появляющееся в онлайн энциклопедии целочисленных последовательностей.

А это наборы из десятков тысяч математических последовательностей, таких как простые числа, числа Фибоначчи, пифагорейские тройки и т.д.

Исходя из этого определения, первое неинтересное число, наименьшее целое число, которое не отображалось ни в одной из последовательностей, – 11 630. Так как в энциклопедию на постоянной основе добавляются новые последовательности, некоторые из них включают в себя бывшие ранее неинтересными цифры.

Самые интересные парадоксы

9. В баре всегда есть хотя бы один клиент, для которого верно, что если пьёт он, значит пьют все.

Условные утверждения в формальной логике иногда имеют противоречивые интерпретации, а парадокс пьянства – отличный тому пример. На первый взгляд, парадокс предполагает, что один человек заставляет пить остальную часть бара.

Фактически всё это говорит о том, что было бы невозможно, чтобы все в баре пили, если бы каждый отдельно взятый клиент не пил. Поэтому там есть по крайней мере один клиент (то есть последний, который не пьёт), который выпив, мог бы сделать так, чтобы можно было сказать, что пьют все.

10. Из мяча, который можно разрезать на конечное число частей, реально сделать два других мяча одинакового размера.

Парадокс Банаха-Тарского опирается на множество странных и противоречивых свойств бесконечных множеств и геометрических вращений.

Части, на которые можно разрезать мяч, будут выглядеть очень странно, поэтому парадокс работает только в абстрактной математической сфере. Было бы отлично, если можно было взять, к примеру, яблоко, разрезать его на части и собрать два одинаковых, но меньшего размера, чтобы поделиться с другом.

Но физические “шары” из материального мира не могут быть разобраны как математическая сфера.

Странные парадоксы

11. Картофель весом в 100 граммов – это 99 процентов воды. Если он высохнет на 1 процент, то его новый вес составит 50 граммов.

Даже при работе по устаревшим методам с конечными величинами, математика может привести к странным результатам.

Чтобы понять картофельный парадокс, нужно внимательно взглянуть на количество содержащейся в картофеле воды.

Поскольку картошка на 99 процентов – это вода, то сухие компоненты получается равны 1 проценту. Вес картофеля – 100 граммов, следовательно, вес сухого материала – 1 грамм.

Когда 100 граммов картофеля высушивается до 98 процентов воды, то 1 грамм сухого компонента превращается в 2 грамма. А один грамм – это два процента от 50 граммов, таким и должен быть новый вес картофелины.

12. Если в комнате находятся 23 человека, очень высоки шансы, что, как минимум, двое из них родились в один и тот же день.

Ещё один удивительный математический результат: парадокс дня рождения исходит из тщательного анализа связанных с этим вероятностей.

Если в комнате находятся два человека, то вероятность того, что у них день рождения в один и тот же день, равна 1/365 (без учёта високосных лет), потому как помимо дня рождения одного человека, в году есть ещё 364 других дня, любой из которых может быть днём рождения второго человека.

Если в комнате три человека, то вероятность того, что у них у всех разные дни рождения равна 364/365 x 363/365. То есть когда мы знаем день рождения первого человека, на выбор даты рождения второго остаётся 364 дня, а для третьего – 363 дня.

Продолжая таким образом, мы доходим до количества в 23 человека, и обнаруживаем, что вероятность того, что у всех людей будут разные дни рождения опускается ниже 50 процентов, поэтому вероятность двух одинаковых дней рождения существенно повышается.

13. У друзей большинства людей больше друзей, чем у них самих.

Это кажется невозможным, но когда вы смотрите на вопрос с математической точки зрения, всё становится понятно. Наглядным примером данного парадокса служат социальные сети, в которых у большинства людей мало друзей. Но некоторые из них – это очень общительные люди, поэтому друзей у них очень много.

Эти люди очень часто “показываются” в качестве “друзей моих друзей”, поэтому они и поднимают среднее их количество.

14. Физик, занимающийся изобретением машины времени, посещает “старую” версию себя. Эта “версия” даёт ему идеи по созданию машины времени, а “молодая” версия использует эти идеи для создания непосредственно аппарата, со времени возвращаясь к старой версии себя.

Путешествие во времени, если это будет возможно, может привести к очень странным ситуациям.

Парадокс Бутстрапа – это противоположность классического парадокса дедушки. Для того, чтобы вернуться назад и не позволить себе путешествовать во времени, некоторая информация и объекты возвращаются во времени, и дают возможность позже вернуться молодой версии себя.

И тут появляется вопрос: каким образом в первый раз появились эта информация и объект. Данный парадокс обсуждали еще в 1941 году. Роберт Хайнлайн (Robert Heinlein) был одним из первых, кто поднял эту тему.

Использование данного парадокса – это не редкость в научной фантастике, а своё название парадокс взял как раз из рассказа Роберта Хайнлайна.

15. Если на Земле нет ничего уникального, тогда в нашей галактике должно существовать много инопланетных цивилизаций. Однако, люди пока не нашли доказательства наличия другой разумной жизни во Вселенной.

Некоторые люди считают молчание нашей Вселенной парадоксом. Одно из основополагающих предположений астрономии: планета Земля – это довольно обычная планета с общей солнечной системой в общей галактике, которая не является чем-то космически уникальным.

Спутник NASA обнаружил, что в нашей галактике, вероятно, есть около 11 миллиардов подобных Земле планет. Учитывая это, жизнь, подобная нам, должна была развиться где-то не слишком далеко от нас (по крайней мере, в космическом масштабе).

Но несмотря на существование мощнейших телескопов, люди не смогли обнаружить существование ни одной технологической цивилизации нигде во Вселенной. Цивилизации шумны: человечество транслирует телевизионные и радиосигналы, которые однозначно искусственны.

Такая цивилизация, как наша, должна давать признаки своего существования, которые люди бы нашли, если бы они существовали.

Более того, цивилизация, возникшая миллионы лет назад (довольно недавно с космической точки зрения), имела достаточно времени для того, чтобы хотя бы начать колонизировать галактику, а это означает, что свидетельств её существования должно быть ещё больше.

Действительно, имея в распоряжении такое количество времени, колонизирующая цивилизация смогла бы колонизировать всю Галактику. Физик Энрико Ферми (Enrico Fermi), в честь которого был назван этот парадокс, как-то во время обеденного перерыва с коллегами спросил: “Где они?”

Одно из решений парадокса бросает вызов вышеизложенной идее и говорит о том, что сложные жизни – это крайне редкая вещь во Вселенной. Другая теория утверждает, что технологические цивилизации неизбежно уничтожаются в результате ядерной войны или экологического разрушения.

Более оптимистичным решением является идея о том, что инопланетяне намеренно скрываются от нас, пока мы не станем более социально и технологически зрелыми. Ещё одна теория гласит, что чужеродные технологии настолько развиты, что мы даже не можем их распознать.

Парадоксы Зенона Элейского

Зенон Элейский – греческий логик и философ, который в основном известен по парадоксам, названным в его честь. О его жизни известно не очень много. Родной город Зенона – Элея. Также в трудах Платона упоминалась встреча философа с Сократом.

Примерно в 465 году до н. э. Зенон написал книгу, где подробно изложил все свои идеи. Но, к сожалению, до наших дней она не дошла. Согласно легенде, философ погиб в бою с тираном (предположительно, главой Элеи Неархом). Всю информацию о Элейском собирали по крупицам: из трудов Платона (родившегося на 60 лет позже Зенона), Аристотеля и Диогена Лаэртия, написавшего три века спустя книгу биографий греческих философов. Упоминания о Зеноне есть и в трудах поздних представителей школы греческой философии: Фемистия (4 век н. э.), Александра Афродийского (3 век н. э.), а также Филопона и Симплиция (оба жили в 6 веке н. э.). Причём данные в этих источниках настолько хорошо согласуются между собой, что по ним можно реконструировать все идеи философа. В этой статье мы расскажем вам про парадоксы Зенона. Итак, приступим.

Парадоксы множества

Ещё с эпохи Пифагора пространство и время рассматривались исключительно с точки зрения математики. То есть считалось, что они составлены из множества моментов и точек. Однако у них есть свойство, которое проще ощутить, чем определить, а именно «непрерывность». Некоторые парадоксы Зенона доказывают, что её невозможно разделить на моменты или точки. Рассуждение философа сводится к следующему: «Допустим, что мы провели деление до конца. Тогда верен только один вариант из двух: либо мы получим в остатке минимально возможные величины или части, которые неделимы, но бесконечны в своём количестве, либо деление приведёт нас к частям без величины, так как непрерывность, являясь однородной, должна быть делимой при любых обстоятельствах. Она не может быть в одной части делима, а в другой – нет. К сожалению, оба результата довольно нелепы. Первый из-за того, что процесс деления не может закончиться, пока в остатке есть части, имеющие величину. А второй потому, что в подобной ситуации изначально целое было бы сформировано из ничего». Симплиций приписывал данное рассуждение Пармениду, но более вероятно, что его автор – Зенон. Идём далее.

Парадоксы Зенона о движении

Они рассматриваются в большей части книг, посвящённых философу, поскольку вступают в диссонанс со свидетельствами чувств элеатов. Применительно к движению, выделяют следующие парадоксы Зенона: «Стрела», «Дихотомия», «Ахилл» и «Стадий». И дошли они до нас благодаря Аристотелю. Давайте рассмотрим их подробней.

«Стрела»

Другое название – квантовый парадокс Зенона. Философ утверждает, что любая вещь либо стоит на месте, либо движется. Но ничто не пребывает в движении, если занимаемое пространство равное ему по протяжённости. В определённый момент движущаяся стрела находится на одном месте. Поэтому она не движется. Симплиций сформулировал этот парадокс в краткой форме: «Летящий предмет занимает равное себе место в пространстве, а то, что занимает равное себе место в пространстве, не движется. Следовательно, стрела покоится». Фемистий и Фелопон сформулировали аналогичные варианты.

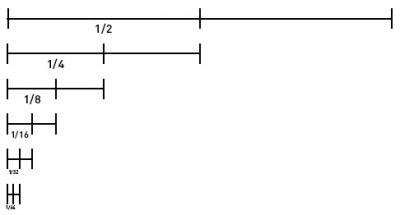
«Дихотомия»

Занимает второе место списка «Парадоксы Зенона». Он гласит следующее: «Прежде чем объект, который начал движение, сможет пройти определённое расстояние, он должен преодолеть половину данного пути, далее половину оставшегося и т. д. до бесконечности. Так как при повторных делениях расстояния пополам отрезок всё время становится конечным, а число данных отрезков бесконечно, то это расстояние невозможно преодолеть за конечное время. Причём данный довод справедлив как в отношении малых расстояний, так и больших скоростей. Следовательно, любое движение невозможно. То есть бегун даже не сможет стартовать».

Этот парадокс очень подробно прокомментировал Симплиций, указав, что в данном случае за конечное время нужно совершить бесконечное количество касаний. «Тот, кто чего-либо касается, может вести счёт, но бесконечное множество нельзя перебрать или сосчитать». Или, как сформулировал Филопон, бесконечное множество неопределимо.

«Ахилл»

Также известен, как парадокс черепахи Зенона. Это наиболее популярное рассуждение философа. В этом парадоксе движения Ахиллес состязается в беге с черепахой, которой на старте даётся небольшая фора. Парадокс в том, что греческому воину не удастся догнать черепаху, так как сначала он добежит до места её старта, а она уже будет на следующей точке. То есть черепаха постоянно будет впереди Ахиллеса.

Этот парадокс очень похож на дихотомию, но здесь бесконечное деление идёт сообразно прогрессии. В случае же дихотомии была регрессия. К примеру, тот же бегун не может стартовать, потому что не может покинуть своего местонахождения. А в ситуации с Ахиллом, даже если бегун тронется с места, он всё равно никуда не прибежит.

«Стадий»

Если сравнивать все парадоксы Зенона по степени сложности, то этот вышел бы победителем. Он труднее прочих поддаётся изложению. Симплиций и Аристотель описали это рассуждение фрагментарно, и нельзя со 100 % уверенностью полагаться на его надёжность. Реконструкция данного парадокса имеет следующий вид: пусть А1, А2, А3 и А4 являются неподвижными телами равного размера, а Б1, Б2, Б3 и Б4 – это тела того же размера, что и А. Тела Б движутся вправо так, что каждое Б минует А за одно мгновение, являющееся наименьшим промежутком времени из всех возможных. Пусть В1, В2, В3 и В4 – тела идентичные А и Б, и движутся относительно А влево, преодолевая каждое из тел за одно мгновение.

Очевидно, что В1 преодолело все четыре тела Б. Примем за единицу время, понадобившееся одному телу В для прохождения одного тела Б. В этом случае на всё передвижение понадобилось четыре единицы. Однако считалось, что два момента, прошедших за это передвижение, минимальны и потому – неделимы. Из этого следует, что четыре неделимых единицы равны двум неделимым единицам.

«Место»

Итак, теперь вы знаете основные парадоксы Зенона Элейского. Осталось рассказать о последнем, который известен под названием «Место». Данный парадокс Зенону приписывает Аристотель. Похожие рассуждения приводились в трудах Филопона и Симплиция в 6 веке н. э. Вот как Аристотель рассказывает об этой проблеме в своей Физике: «Если существует какое-то место, то как определить, где оно находится? Затруднение, к которому пришел Зенон, требует объяснения. Поскольку всё существующее имеет место, то становится очевидным, что и у места должно быть место, и т. д. до бесконечности». По мнению большинства философов, парадокс здесь появляется только потому, что ничто из существующего не может отличаться от самого себя и содержаться само в себе. Филопон считает, что, акцентируя внимание на самопротиворечивости понятия «места», Зенон хотел доказать несостоятельность теории множественности.

Источники:

http://www.syl.ru/article/378494/paradoksyi-zenona-eleyskogo—opisanie-znachenie-i-interesnyie-faktyi
http://www.infoniac.ru/news/15-paradoksov-kotorye-vzorvut-vash-mozg.html
http://fb.ru/article/179798/paradoksyi-zenona-eleyskogo