Какое число делится на 17 24 8. Основные признаки делимости

Признак делимости на 8, примеры, доказательство

В статье рассматривается признак делимости на 8 с приведением его формулировки и примерами.

Признак делимости на 8, примеры

Формулировка звучит так: если число, составленное из последних цифр в записи целого а , делится на 8 тогда и все число делится на 8 ; когда число, составленное из трех последних, не делится на 8 , тогда и все число не делится на число 8 .

Приведенная формулировка говорит о том, что этот признак применим только для четырехзначных, пятизначных и так далее чисел. Данный метод безопасный и удобный, так как после всего можно выполнить проверку. Установка деления на 8 производится при помощи деления выражения на 8 .

Проверить, делится ли 58 296 на 8 .

Для решения задания нужно применить признак делимости на 8 . Для этого нужно взять последние 3 цифры числа и разделить столбиком на 8 . Получаем, что 296 нужно делить на 8 . Имеем, что

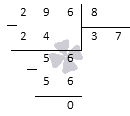
Очевидно, что 296 поделится на 8 без остатка. Тогда заданное число полностью поделится на 8 .

Когда последние три цифры имеют вид 024 , 086 , 002 , 008 , тогда необходимо отбросить нули и выполнять деление двузначных чисел.

При помощи признака делимости на 8 узнать, делится ли 920 072 на 8 .

Видно, что последние три цифры записываются как 072 , значит, будем иметь дело с числом 72 , разделим его на 8 . По признаку делимости видно, что заданное число делится на 8 без остатка.

Определить числа, которые поделятся на 8 из заданных − 900 007 , 21 008 , − 111 008 и 732 237 001 .

Воспользовавшись признаком делимости на 8 , нужно пересмотреть все цифры, находящиеся справа числа, то есть 007 , 008 , 008 , 001 . Отсюда видно, что будем работать с числами 7 , 8 , 8 , 1 . Очевидно, что только 8 поделится само на себя, значит, из выбранных только 21008 и – 111008 поделятся на 8 .

Ответ: − 900 007 и 732 237 001 на 8 не делятся, а 21 008 и − 111 008 делятся на 8 .

Когда записанное число имеет справа последние три цифры нули, то есть 23000 , – 980000 , тогда очевидно, что все число делится на 8 . Рассмотрим доказательство данного утверждения.

Число 1000 можно представить как 1 000 = 8 · 125 . Видно, что оно точно поделится на 8 .

Когда имеются числа, где в конце записаны 3 нуля, то очевидно, что нужно использовать правило умножения натуральных чисел на 1000 , которое поможет представить а в виде a = a 1 · 1 000 . Отсюда видно, что a 1 получим из числа а , когда заберем последние три цифры, расположенные справа. Очевидно, что 1000 делится на 8 , тогда и выражение a 1 · 1 000 будет делиться на 8 по свойствам делимости. Отсюда получили, что число а будет делиться на 8 без остатка.

Теперь делимость числа на 8 доказана, когда число оканчивается на три нуля. Благодаря свойству делимости, это утверждение верно для всех натуральных а .

Доказательство признака делимости на 8

Для доказательства делимости на 8 необходимо использовать представление натурального числа а , то есть любое число представить в виде a = a 1 · 1 000 + a 0 , где a 1 – это результат отбрасывания последних трех цифр, а a 0 – это есть последние цифры числа а . Для полного понятия запишем, что 234 698 = 234 · 1 000 + 698 .

Для доказательства нужно применять свойства делимости:

• для деления нацело числа а на b необходимо и достаточно, чтобы модель числа а делился на модуль числа b ;
• когда из равенства a = s + t все члены могут делиться на b , тогда и заданный член делится на b .

Переходим к доказательству признака делимости на 8 с достаточными и необходимыми условиями.

Чтобы целое число поделилось на 8 , необходимо и достаточно, чтобы число, состоящее из последних трех цифр записи числа а , делилось на 8 .

Пусть целое число обозначим за а . Тогда модуль числа а является натуральным числом. Необходимо представить его в виде a = a 1 · 1000 + a 0 .

Перейдем к доказательству необходимости. Пусть число а делится на 8 . Тогда нужно составить такое число, которое будет составлено из тех последних цифр заданного числа а , делящееся на 8 Отсюда получим, что a 0 делится на 8 .

Если а делится на 8 , тогда и его модуль тоже, исходя из первого свойств делимости. Исходя из равенства вида a = a 1 · 1000 + a 0 получим, что a 1 · 1 000 поделится на 8 , а по второму свойству делимости видно, что a 0 поделится на 8 без остатка. Необходимость доказана.

Доказательство достаточности начинается с того, что необходимо взять за a число, которое делится на 8 . Это приведет к тому, что и число а будет делиться на 8 .

Видно, что из равенства a = a 1 · 1000 + a 0 произведение вида a 1 · 1 000 поделится на 8 , что означает, a 0 также будет делиться на 8 . Делаем вывод, что и само число будет делиться на 8 . Достаточность доказана.

Другие случаи делимости на 8

Не всегда возможно установить делимость на 8 сразу, так как либо число, либо выражение не представлено в явном виде. Поэтому следует предварительно выполнить несколько преобразований.

Когда имеется буквенное выражение а , следует выяснить, будет ли выражение делиться на 8 , возникают трудности. В этом случае, исходя из свойства, все выражение должно делиться на 8 . Рассмотрим на примере.

Чаще всего, если имеется произведение, лучше применять формулу бинома Ньютона.

Выяснить, делится ли выражение вида 9 n + 16 n – 9 на 8 при n являющимся натуральным числом.

Нужно представить 9 как 8 + 1 и применить формулу бинома Ньютона. Тогда получаем выражение:

9 n + 16 n – 9 = ( 8 + 1 ) + 16 n – 9 = = ( C n 0 · 8 n + C n 1 · 8 n – 1 · + . . . + + C n n – 2 · 8 2 · 1 n – 2 + C n n – 1 · 8 · 1 n – 1 + C n n · 1 n ) + 16 n – 9 = = ( 8 n + C n 1 · 8 n – 1 + . . . + C n n – 2 · 8 2 + n · 8 + 1 ) + 16 n – 9 = = 8 n + C n 1 · 8 n – 1 + . . . + C n n – 2 · 8 2 + 24 n – 8 = = 8 · ( 8 n – 1 + C n 1 · 8 n – 2 + . . . + C n n – 2 · 8 1 + 3 n – 1 )

Получили результат, который делится на 8 , потому как имеется множитель в виде числа 8 , причем значение в скобках равняется натуральному числу n . Отсюда получаем, что данное по условию выражение будет делиться на 8 при любому натуральном значении n .

Заданное выражение можно разложить на множители или оно уже задается в таком виде. Следует учитывать то, что значение выражения с n при n = 8 · m , n = 8 · m + 1 , … , n = 8 · m + 7 , где m является целым числом, будет делиться на 8 , тогда и само заданное выражение поделится на 8 при любом целом значении n .

Доказать, что выражение вида n 5 + 7 · n 3 будет делиться на 8 при любом целом значении n .

Перейдем к разложению на множители выражения n 5 + 7 · n 3 = n 3 · ( n 2 + 7 )

Если n = 8 m , тогда получим, что:

n 3 · ( n 2 + 7 ) = ( 8 m ) 3 · 8 m 2 + 7 = 8 3 · m 3 · ( 64 m 2 + 7 )

Выражение будет делиться на m без остатка при любом целом значении числа m, потому как имеется множитель вида 8 3 , который тоже делится на 8 .

Когда n = 8 · m + 1 , получим, что

n 3 · ( n 2 + 7 ) = ( 8 m ) 3 · 8 m 2 + 7 = ( 8 m + 1 ) 3 · ( 64 m 2 + 16 m + 8 ) = = ( 8 m + 1 ) 3 · 8 · ( 8 m 2 + 2 m + 1 )

Значение такого произведения делится на 8 , когда m принимает значение любого целого числа, потому как в записи имеется множитель 8 .

Таким же образом выполняется при n = 8 · m + 2 , n = 8 · m + 3 , … , n = 8 · m + 7 , тогда получаем, что произведения также поделятся на 8 .

Мы доказали, что выражение, заданное по условию, будет делиться на 8 без остатка при любом целом n .

Имеются случаи, когда необходимо применять метод математической индукции.

Доказать при помощи математической индукции, что при n , равному любому натуральному числу, выражение вида 9 n + 16 n – 9 будет делиться на 8 .

Необходимо провести проверку при значении n = 1 , чтобы исходное выражение делилось на 8 Тогда получим, что 9 1 + 16 · 1 – 9 = 16 . Очевидно, что результат, равный 16 , делится на 8 без остатка.

Если предположить, что значение n = k , тогда выражение вида 9 n + 16 n – 9 делится на 8 и приобретает вид 9 k + 16 k – 9 , который также делится на число 8 .

По заданному предположению необходимо доказать, что 9 k + 16 k – 9 поделится на 8 , а исходное выражение поделится на 8 при значении n = k + 1 .

Тогда получим, что:

9 k + 1 + 16 · ( k + 1 ) – 9 = 9 · 9 k + 16 k + 7 = 9 · ( 9 k + 16 k – 9 ) – 128 k + 88 = = 9 · ( 9 k + 16 k – 9 ) – 8 · ( 16 k – 11 )

Видно, что полученная разность выражений вида 9 · ( 9 k + 16 k – 9 ) будет делиться на 8 , потому как 9 k + 16 k – 9 поделится на 8 , а произведение 8 · ( 16 k – 11 ) , исходя из выше написанного, также поделится на 8 , потому как имеет множитель в виде числа 8 . Отсюда следует, что полученная разность поделится на 8 . Видно, что искомая делимость на 8 найдена из выражения вида 9 k + 1 + 16 · ( k + 1 ) – 9 .

Данный пример был решен при помощи метода математической индукции, была доказана делимость выражения 9 n + 16 n – 9 на 8 без остатка, где n является любым целым натуральным числом.

Признаки делимости

Содержание

1. Что такое делимость?
2. Признаки делимости
3. На 2,4,8
4. На 3 и 9
5. На 5
6. На 6
7. На 7
8. На 10
9. На 11
10. Что мы узнали?

Бонус

• Тест по теме

Что такое делимость?

Признаки делимости позволяют просто и быстро определить, возможно ли полностью поделить одно число на другое. А делимость это и есть возможность поделить одно число на друге без остатка.

Признаки делимости

Признаки делимости удобнее изучать, разбив возможные делители на группы. Поступим так же и рассмотрим делимость на каждую из групп в отдельности.

На 2,4,8

Эти числа в рассматриваемом вопросе сгруппированы, так как их признаки очень похожи друг на друга.

• Число делится на 2 только если является четным.
• Число делится на 4, если последние две цифры числа делятся на 4 или последние две цифры 00. Например, число 130 не делится на 4, так как 30 не делится на 4. А вот уже число 1400 можно поделить на 4.
• Число делится на 8, если последние две цифры числа нули или делятся на 8

На 3 и 9

Число делится на 3, если сумма цифр этого числа делится на 3. Рассмотрим число: 804. Оно делится на 3, поскольку сумма цифр 8+0+4=12 – делится на 3.

Число делится на 9, если сумма цифр числа делится на 9.

Число делится на 5, если последняя цифра числа равняется 5 или нулю. Это наиболее известный признак делимости, наряду с делимостью на 2.

Чтобы число делилось на 6, оно должно делиться на 2 и 3, так как 2*3=6. Поэтому признак делимости на 6 это объединение признаков деления на 2 и на 3.

То есть: число делится на 6, если оно четное и сумма всех его цифр делится на 3

Самые сложные в восприятии признаки делимости на 7 и на 11. Число делится на 7, если разность сумм четных цифр числа и нечетных цифр чисел делится на 7.

Приведем пример: число 469 делится на 7. Почему? Сумма цифр на нечетных позициях 4+9=13. Сумма чисел на четных позициях 6. Разность получившихся сумм: 13-6=7, а это число делится на 7. Поэтому все число 469 делится на 7

На 10

Число делится на 10 только если последней цифрой числа является 0

По тому же принципу определяют делимость числа на 100, 1000 и так далее. Если у числа два нуля на конце, то оно делится на 100, если три нуля на конце, число делится на 1000 и так далее.

На 11

Число делится на 11 только, если разность сумм четных и нечетных цифр числа делится на 11 или равняется нулю Приведем пример:

Число 2035 делится на 11. Сумма цифр, стоящих на четных позициях: 2+3=5. Сумма нечетных цифр: 0+5=5. Разность полученных выражений:5-5=0, значит число делится на 11.

Нельзя путать понятия четной позиции и четного числа. Цифра это знак, который используется для записи чисел. Число это набор цифр, каждая из которых стоит на своей позиции. В числе 127 всего три цифры. Цифра 1 стоит на первой позиции, цифра 2 на второй и так далее. На четной позиции находится цифра 2. На нечетных позициях цифры 1 и 7.

Чтобы быстрее запомнить все группы можно свести в таблицу признаков делимости чисел.

Основные признаки делимости.

Признак делимости – правила с помощью которого можно относительно бегло найти, является ли число кратным предварительно выбранному. Если для двух целых чисел m и n имеется такое целое число k и nk=m, то число m делится на n

Применение навыков делимости упрощает вычисления, и соразмерно повышает скорость их исполнения. Разберем детально основные характерные особенности делимости.

Наиболее незамысловатый признак делимости для единицы: на единицу делится все числа. Так же элементарно и с признаками делимости на два, пять, десять. На два можно поделить четные число либо то у которого итоговая цифра 0, на пять – число у которого конечная цифры 5 или 0. На десять поделятся только те числа, у которых заключительная цифра 0, на 100 — только те числа, у которых две заключительных цифры нули, на 1000 — только те, у которых три заключительных нуля.

Цифру 79516 можно разделить на 2, так как она заканчивается на 6— четное число; 9651 не поделится на 2, так как 1 – цифра нечетная; 1790 поделится на 2, так как конечная цифра нуль. 3470 поделится на 5 (заключительная цифра 0); 1054 не поделится на 5 (конечная цифра 4). 7800 поделится на 10 и на 100; 542000 поделится на 10, 100, 1000.

Менее широко известны, но весьма удобны в использовании характерные особенности делимости на 3 и 9, 4, 6 и 8, 25. Имеются так же характерные особенности делимости на 7, 11, 13, 17, 19 и так далее, но ими пользуются на практике значительно реже.

Характерная особенность деления на 3 и на 9.

На три и/или на девять без остатка разделятся те числа, у которых результат сложения цифр кратен трем и/или девяти.

Число 156321, результат сложения 1 + 5 + 6 + 3 + 2 + 1 = 18 поделится на 3 и поделится на 9, соответственно и само число можно поделить на 3 и 9. Число 79123 не поделится ни на 3, ни на 9, так как сумма его цифр (22) не поделится на эти числа.

Характерная особенность деления на 4, 8, 16 и так далее.

Цифру можно без остатка разделить на четыре, если у нее две последние цифры нули или являются числом, которое можно поделить на 4. Во всех остальных вариантах деление без остатка не возможно.

Число 75300 поделится на 4, так как последние две цифры нули; 48834 не делится на 4, так как последние две цифры дают число 34, не делящееся на 4; 35908 делится на 4, так как две последние цифры 08 дают число 8, делящееся на 4.

Схожий принцип пригоден и для признака делимости на восемь. Число делится на восемь, если три последние его цифры нули или образуют число, делящееся на 8. В прочих случаях частное, полученное от деления, не будет целым числом.

Такие же свойства для деления на 16, 32, 64 и т. д., но в повседневных вычислениях они не используются.

Характерная особенность делимости на 6.

Число делится на шесть, если оно делится и на два и на три, при всех прочих вариантах, деление без остатка невозможно.

126 поделится на 6, так как оно делится и на 2 (заключительное четное число 6), и на 3 (сумма цифр 1 + 2 + 6 = 9 делится на три)

Характерная особенность делимости на 7.

Число делится на семь если разность его удвоенного последнего числа и “числа, оставшегося без последней цифры”делится на семь, то и само число делится на семь.

Число 296492. Возьмем последнюю цифру “2”, удваиваем, выходит 4. Вычитаем 29649 – 4 = 29645. Проблематично выяснить делится ли оно на 7, следовательно анализируемом снова. Далее удваиваем последнюю цифру “5”, выходит 10. Вычитаем 2964 – 10 = 2954. Результат тот же, нет ясности, делится ли оно на 7, следовательно продолжаем разбор. Анализируем с последней цифрой “4”, удваиваем, выходит 8. Вычитаем 295 – 8 = 287. Сверяем двести восемьдесят семь – не делится на 7, в связи с этим продолжаем поиск. По аналогии последнюю цифру “7”, удваиваем, выходит 14. Вычитаем 28 – 14 = 14. Число 14 делится на 7, итак исходное число делится на 7.

Характерная особенность делимости на 11.

На одиннадцать делятся только те числа, у которых результат сложения цифр, размещающихся на нечетных местах, либо равен сумме цифр, размещающихся на четных местах, либо отличен на число, делящееся на одиннадцать.

Число 103 785 делится на 11, так как сумма цифр, размещающихся на нечетных местах, 1 + 3 + 8 = 12 равна сумме цифр, размещающихся на четных местах 0 + 7 + 5 = 12. Число 9 163 627 делится на 11, так как сумма цифр, размещающихся на нечетных местах, есть 9 + 6 + 6 + 7 = 28, а сумма цифр, размещающихся на четных местах, есть 1 + 3 + 2 = 6; разность между числами 28 и 6 есть 22, а это число делится на 11. Число 461 025 не делится на 11, так как числа 4 + 1 + 2 = 7 и 6 + 0 + 5 = 11 не равны друг другу, а их разность 11 – 7 = 4 не делится на 11.

Характерная особенность делимости на 25 .

На двадцать пять поделятся числа, две заключительные цифры которых нули или составляют число, которое можно разделить на двадцать пять (т. е. числа, оканчивающиеся на 00, 25, 50 или 75). При прочих вариантах – число невозможно поделить целиком на 25.

9450 поделится на 25 (оканчивается на 50); 5085 не делится на 25.

Источники:

http://zaochnik.com/spravochnik/matematika/delimost/priznak-delimosti-na-8/
http://obrazovaka.ru/matematika/priznaki-delimosti-tablica-s-primerami.html
http://www.calc.ru/Osnovnyye-Priznaki-Delimosti.html