Деление на 9 и 3. Приведем несколько примеров

Признаки делимости на 3 и на 9

Рассмотрим простенькую задачу. В одном хозяйстве было собрано утром 846 куриных яиц. Хозяйство это было общим, его содержит 9 семей. Надо разделить между ними поровну все яйца. Как проверить, не выполняя деление, делится ли число 846 на 9 без остатка.

Сначала разложим данное число по разрядам. Число 846 состоит из 8 сотен, 4 десятков и 6 единиц.

Начнем разбираться с сотнями. Если в 100 яиц раскладывать по девяти корзинам, то у нас останется одной яйцо лишнее. То есть с каждой сотни яиц будет 1 яйцо. Так как у нас 8 сотен целых, то следовательно останется 8 яиц.

Теперь разберемся с десятками. Если десять яиц раскладывать по девяти корзинам, то тоже останется одно лишнее яйцо, с каждого десятка. Так как в нашем числе десятков 4, то следовательно останется 4 яйца.

6 яиц которые были в разряде единиц, мы никак не сможем разложить по девяти корзинам, следовательно они тоже останутся.

Теперь сложим все яйца, которые у нас остались. 8 от сотен, 4 от десятков и 6 от единиц, в сумме 8+4+6=18 яиц. 18 яиц можно разложить по девяти корзинам, и не останется ни одного лишнего яйца. Следовательно 846 яиц можно разложить поровну по девяти корзинам. Это значит, что число 846 делится без остатка на 9.

Признак делимости на 9

Теперь, можем сформулировать признак делимости числа на 9.

• Если сумма цифр числа делится без остатка на 9, то и само число делится на 9. Если сумма цифр числа не делится без остатка на 9, то и само число не будет делиться на 9 без остатка.

Приведем несколько примеров:

Число 76 005 будет делиться без остатка на 9, так как сумма составляющих его цифр: 7+6+0+0+5=18 делится на 9 без остатка.

Число 51 734 не делится без остатка на 9, так как сумма составляющих его цифр: 5+1+7+3+4=20 не делится на 9 без остатка.

Признак делимости на 3

Аналогичным образом получим признак делимости числа на 3.

От деления сотни на 3, будет оставаться единица. От деления десятки на 3, тоже будет оставаться единица. Получаем копию ситуации с девяткой.

• Если сумма цифр числа делится без остатка на 3, то и само число делится на 3. Если сумма цифр числа не делится без остатка на 3, то и само число не будет делиться на 3 без остатка.

Число 76 005 будет делиться без остатка на 3, так как сумма составляющих его цифр: 7+6+0+0+5=18 делится на 3 без остатка.

Число 51 734 не делится без остатка на 3, так как сумма составляющих его цифр: 5+1+7+3+4=20 не делится на 3 без остатка.

Признак делимости на 9, примеры, доказательство.

Продолжаем изучать признаки делимости. На очереди признак делимости на 9. Сейчас мы дадим его формулировку, разберем примеры его применения для установления делимости на 9 данного целого числа и приведем доказательство признака делимости на 9 . В заключение остановимся на доказательстве делимости на 9 значений выражения с переменной при различных значениях переменной.

Навигация по странице.

Признак делимости на 9, примеры

Для начала сформулируем признак делимости на 9: если сумма цифр целого числа делится на 9 , то и само число делится на 9 ; если же сумма цифр числа не делится на 9 , то это число не делится на 9 .

Из приведенной формулировки понятно, что для использования признака делимости на 9 необходимо знать, как выполняется сложение натуральных чисел. Еще для применения признака делимости на 9 нужно знать, что из однозначных натуральных чисел на 9 делится только число 9 , а числа 1 , 2 , 3 , 4 , 5 , 6 , 7 и 8 на 9 не делятся.

Теперь можно рассмотреть простейшие примеры применения признака делимости на 9.

Какие из чисел 621 , −32 112 , 222 , −331 делятся на 9 ?

Вычислим суммы цифр каждого из данных чисел, имеем 6+2+1=9 , 3+2+1+1+2=9 , 2+2+2=8 и 3+3+1=7 . Так как 9 делится на 9 , а 8 и 7 не делятся на 9 , то признак делимости на 9 позволяет утверждать, что 621 и −32 112 делятся на 9 , а числа 222 и −331 – нет.

В более сложных случаях сумма цифр данного целого числа может быть двухзначным, трехзначным и т.д. числом. Например, сумма цифр числа 945 равна 18 , а сумма цифр числа 999 888 777 666 555 равна 105 . Для установления делимости на 9 в этих случаях признак делимости на 9 приходится применять несколько раз (точнее приходится несколько раз подряд вычислять суммы цифр получающихся чисел). Рассмотрим это на примере.

Делится ли число 876 505 998 872 на 9 ?

Воспользуемся признаком делимости на 9 . Для этого вычислим сумму цифр данного числа: 8+7+6+5+0+5+9+9+8+8+7+2=74 . А делится ли 74 на 9 ? Для ответа на этот вопрос вычислим сумму цифр числа 74 , имеем 7+4=11 , а сумма цифр числа 11 в свою очередь равна 1+1=2 . Так как 2 не делится на 9 , то по признаку делимости на 9 и число 11 не делится на 9 , следовательно, на 9 не делится и 74 , а значит, и исходное число.

Отметим также, что проверить способность данного числа делиться на 9 можно, непосредственно разделив данное число на 9 (удобнее всего выполнить деление столбиком). Достаточно часто на выполнение непосредственного деления уходит примерно столько же времени, как и на применение признака делимости на 9 .

Доказательство признака делимости на 9

Для доказательства признака делимости на 9 нам потребуются несколько вспомогательных результатов. Обговорим их.

Любое натуральное число a мы можем разложить по разрядам, после чего правила умножения натурального числа на 10, 100, 1 000 позволяют нам записать представление числа a вида a=a_n·10 n +a_n−1·10 n−1 +…+a₂·10 2 +a₁·10+a , где a_n, a_n−1, …, a – цифры, стоящие слева направо в записи числа a . Так как 10=9+1 , 100=99+1=11·9+1 , 1 000=999+1=111·9+1 , …, то представление числа a примет вид . После небольших преобразований приходим к равенству вида . Сумма представляет собой сумму цифр числа a . Обозначим ее для краткости буквой A , тогда . Это представление числа a мы и будем использовать при доказательстве признака делимости на 9 .

Также нам пригодятся два свойства делимости:

• чтобы целое число a делилось на целое число b необходимо и достаточно, чтобы модуль числа a делился на модуль числа b ;
• если в равенстве a=s+t все члены, кроме какого-то одного, делятся на некоторое целое число b , то и этот один член делится на b .

Вот теперь можно провести доказательство признака делимости на 9. Для удобства перепишем этот признак в виде необходимого и достаточного условия делимости на 9 .

Для делимости целого числа a на 9 необходимо и достаточно, чтобы сумма цифр в записи числа a делилась на 9 .

Для a=0 теорема очевидна.

Для a , отличных от нуля, модуль числа a является числом натуральным, поэтому его можно представить в виде суммы , что мы показали перед теоремой. В выражении содержится множитель 9 , а сумма в скобках является натуральным числом при любых a_n, a_n−1, …, a₁ , поэтому в силу свойств делимости указанное выражение делится на 9 .

Приступаем к доказательству достаточности. Докажем, что если сумма цифр числа a (которую мы обозначили как A ) делится на 9 , то число a делится на 9 .

Если A делится на 9 , то из равенства и второго указанного перед теоремой свойства делимости следует, что модуль a делится на 9 , откуда в силу первого указанного перед теоремой свойства делимости следует, что и a делится на 9 . Так доказана достаточность.

Переходим к доказательству необходимости. Докажем, что если целое число a делится на 9 , то сумма его цифр делится на 9 .

Если a делится на 9 , то и модуль числа a делится на 9 (по первому указанному перед теоремой свойству делимости). Тогда из равенства и второго указанного свойства делимости следует, что А делится на 9 . Так доказана необходимость.

На этом доказательство признака делимости на 9 завершено.

Другие случаи делимости на 9

В этом пункте мы хотим затронуть примеры доказательства делимости на 9 , когда число задано в виде значения буквенного выражения при некоторых значениях переменной.

Делится ли 10 n −1 на 9 при любом натуральном n ?

Достаточно очевидно, что 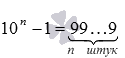. Сумма цифр числа равна 9·n , а 9·n делится на 9 , следовательно, по признаку делимости на 9 можно говорить о делимости 10 n −1 на 9 при любом натуральном n .

Однако во многих случаях воспользоваться признаком делимости на 9 не представляется возможности, также как и выполнить деление на 9 . В таких случаях логично попробовать представить исходное выражение в виде произведения нескольких целых множителей, один из которых делится на 9 . Покажем два способа получения такого произведения.

Иногда получить произведение нужного вида позволяет формула бинома Ньютона. Рассмотрим пример.

Делится ли 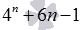на 9 при любом натуральном n ?

Представим 4 как 3+1 , применим формулу бинома Ньютона и проведем преобразования:

При n=1 имеем , а 9 делится на 9 . При натуральных n , больших единицы, в полученной сумме можно вынести 9 за скобки, при этом мы придем к произведению . Это произведение делится на 9 , так как содержит множитель 9 , а значение выражения в скобках при n>1 является натуральным числом. Таким образом, 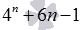делится на 9 при любом натуральном n .

Когда исходное выражение с переменной n задано в виде многочлена, то можно пробовать такой подход. Если доказать, что при n=9·m , n=9·m+1 , …, n=9·m+8 , где m – целое число, исходное выражение делится на 9 , то этим будет доказана делимость исходного выражения на 9 при любом целом n .

Докажите, что 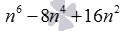делится на 9 при любом целом n .

Для удобства разложим на множители выражение :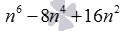

Пусть m – целое число.

При n=9·m получаем . Полученное произведение делится на 9 , так как множитель (9·m) 2 очевидно делится на 9 .

Полученное произведение делится на 9 , так как содержит множитель 9 .

Аналогично показывается делимость на 9 выражения 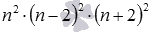при n=9·m+2 , n=9·m+3 , …, n=9·m+8 .

Так доказана делимость на 9 значения исходного выражения при любом целом n .

Наконец, доказать делимость на 9 в некоторых случаях позволяет метод математической индукции. Вот тому подтверждение в виде примера.

Докажите, что 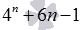при любом натуральном n делится на 9 .

Для доказательства воспользуемся методом математической индукции.

При n=1 значение выражения 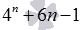равно 9 , и оно, очевидно, делится на 9 .

Предположим, что при n=k значение выражения 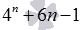делится на 9 , то есть, будем считать, что делится на 9 .

Исходя из предположения предыдущего шага, докажем, что 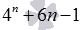делится на 9 при n=k+1 .

В полученной разности 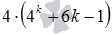делится на 9 , так как мы предположили на предыдущем шаге, что делится на 9 ; а тоже делится на 9 , так как содержит множитель 9 . Следовательно, и вся разность делится на 9 , а значит и значение выражения 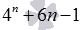при n=k+1 делится на 9 .

Так методом математической индукции доказано, что 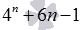делится на 9 при любом натуральном n .

Признак делимости на 9, примеры, доказательство

В данной статье будет дана формулировка признака делимости на 9 с его доказательством. Заключительным этапом будет приведение примера делимости на 9 с разным значением переменной.

Признак делимости на 9, примеры

Рассмотрим сам признак делимости на 9 : когда сумма цифр целого числа делится на 9 , тогда само число также делится на 9 ; когда сумма цифр не делится на 9 , тогда очевидно, что и число не будет делиться на 9 .

Для того, чтобы использовать данный признак делимости, необходимо разбираться в сложении натуральных чисел. Известно, что из простых натуральных чисел существует только число 9 , которое способно поделиться на 9 без остатка, то есть подходит под выше написанное определение.

Определить, какие из приведенных чисел 621 , − 32 112 , 222 , − 331 поделятся на 9 без остатка.

Для решения задания необходимо перейти к вычислению сумм каждого из предложенных чисел. Получаем, что 6 + 2 + 1 = 9 , 3 + 2 + 1 + 1 + 2 = 9 , 2 + 2 + 2 = 8 и 3 + 3 + 1 = 7 . Видно, что только 9 поделится на 9 , а 8 и 7 нет. Отсюда имеем, что 621 и – 32112 поделятся на 9 а 222 и – 331 не поделятся.

Ответ: 621 и − 32 112 .

Бывают случаи, когда сумма цифр является трехзначным числом. Когда имеем число 945 , то сумма его цифр – это 18 , а сумма цифр 999888777666555 равняется 105 . Тогда для установления делимости на 9 нужно применять правило несколько раз.

Определить, делится ли число 876 505 998 872 на 9 .

Необходимо воспользоваться признаком делимости на 9 . Переходим к вычислению суммы цифр заданного числа. Тогда получим, что 8 + 7 + 6 + 5 + 0 + 5 + 9 + 9 + 8 + 8 + 7 + 2 = 74 . Чтобы определить, будет ли делиться 74 на 9 ,нужно найти сумму цифр. Тогда получаем, что 7 + 4 = 11 , а 1 + 1 = 2 . Отсюда следует, что 2 не поделится на 9 . То есть число 74 на 9 не делится.

Ответ: не делится.

Чтобы проверить, будет делиться число на 9 или нет, нужно произвести деление на 9 . Применение признака делимости на 9 и непосредственное деление на 9 занимает практически одно и то же время.

Доказательство признака делимости на 9

Чтобы доказать признак делимости на 9 , нужно использовать дополнительные результаты.

Когда разложим по рядам любое натуральное число а , правила умножения натурального числа на 10 , 100 , 1000 позволяет представить все при помощи записи a = a n · 10 n + a n − 1 · 10 n − 1 + … + a 2 · 10 2 + a 1 · 10 + a 0 , где a n , a n − 1 , … , a 0 являются цифрами, записанных слева направо. Имеем, что 10 = 9 + 1 , 100 = 99 + 1 = 11 · 9 + 1 , 1 000 = 999 + 1 = 111 · 9 + 1 , … , тогда число а можно представить в виде a = a n · 11 . . . 1 · 9 + 1 + . . . + a 2 · 11 · 9 + 1 + a 1 · ( 1 · 9 + 1 ) + a 0 .

Нужно преобразовать выражения до вида a = 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 + a n + . . . + a 2 + a 1 + a 0 .

Отсюда получаем, что сумма a n + . . . + a 2 + a 1 + a 0 является суммой всех цифр, входящих в состав числа а . Чтобы запись была краткой, запишем a = 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 + A . Данное преобразование числа а применяется при доказательстве признака делимости на 9 .

Используем 2 свойства делимости:

• для возможности деления а на b нужно производить деление модуля а на модуль b ;
• при возможности деления на число b всего выражения a = s + t очевидно, что и все выражение поделится на b .

Рассмотрим само доказательство признака делимости на 9 вместе с необходимыми и достаточными условиями.

Для того, чтобы целое число а делилось на 9 без остатка, необходимо и достаточно, что и сумма цифр числа а делилась на 9 .

При а = 0 теорема очевидна. Если а отлично от нуля, а его модуль – это натуральное число, тогда представим его в виде суммы вида a = 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 + A , что и было представлено задолго до написания теоремы. Выражение 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 имеет множитель 9 , а сумма скобок – это натуральное число при любых a n , a n − 1 , … , a 1 . Видно, что свойство делимости подходит для выражения. Необходимо доказать, что сумма всех цифр ( A ) делится на 9 , тогда и само число разделится на 9 .

Если A делится на 9 , тогда по равенству a = 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 + A и по второму указанному перед теоремой свойству имеем, что и модуль а будет делиться на 9 . Получим, что и само число а будет делиться на 9 . Достаточное свойство доказано.

Доказательство необходимого свойства включает в себя деление на 9 числа а при делении суммы всех цифр числа а .

Когда а будет делиться на 9 , тогда и модуль числа разделится на 9 . Это возможно благодаря первому свойству делимости. Из a = 9 · 11 . . . 1 · a n + . . . + 11 · a 2 + 1 · a 1 + A и второго свойства видно, что A поделится на 9 без остатка. Необходимое свойство доказано.

Другие случаи делимости на 9

Рассмотрим примеры решения примеров с доказательством делимости на 9 , когда имеется буквенное выражение.

Будет ли выражение 10 n − 1 делиться на 9 при натуральном n ?

Видим, что . То есть сумма цифр числа равняется 9 n , а 9 n делится на 9 без остатка. Значит, что выражение соответствует признаку делимости при любом значении n .

Имеются случаи, когда делимость на 9 нельзя определить при помощи деления на 9 . Тогда выражение представляется в виде произведения нескольких множителей, где один из них делится на 9 . Рассмотрим два таких способа. Решим примеры с помощью бинома Ньютона.

Определить, делится ли выражение 4 n + 6 n – 1 на 9 при любом значении n .

Представляем 4 в виде 3 + 1 , используем формулу бинома Ньютона и получим:

4 n + 6 n – 1 = 3 + 1 n + 6 n – 1 = = C n 0 · 3 n + C n 1 · 3 n – 1 · 1 + . . . + C n n – 2 · 3 2 · 1 n – 1 + C n n – 1 · 3 · n – 1 + C n n · 1 n + + 6 n – 1 = = 3 n + C n 1 · 3 n – 1 + . . . + C n n – 2 · 3 2 + n · 3 + 1 + 6 n – 1 = = 3 n + C n 1 · 3 n – 1 + . . . + C n n – 2 · 3 2 + 9 n

Когда n = 1 , получаем, что 4 n + 6 n – 1 = 4 1 + 6 · 1 – 1 = 9 . Очевидно, что 9 делится на 9 . Когда значение n больше 1 , тогда видно, что сумма 3 n + C n 1 · 3 n – 1 + . . . + C n n – 2 · 3 2 + 9 n может быть упрощена при помощи выноса 9 за скобки. Получим выражение вида 9 · 3 n – 2 + C n 1 · 3 n – 3 + . . . + C n n – 2 · 3 0 + n . Очевидно, что произведение поделится на 9 , а значение выражения в скобке удовлетворяет условию n > 1 и является натуральным числом. Отсюда имеем, что 4 n + 6 n – 1 делится на 9 при любых натуральных значениях n .

Если исходное выражение c n переменной в виде многочлена, тогда используется такой способ. При доказательстве n = 9 · m , n = 9 · m + 1 , … , n = 9 · m + 8 , где m является целым числом, а исходное выражение делится на 9 , тогда очевидно, что делимость будет доказана при любом значении n .

Доказать, что n 6 – 8 n 4 + 16 n 2 будет делиться на 9 при любом значении n .

Чтобы удобней было вычислять, нужно выражение n 6 – 8 n 4 + 16 n 2 разложить на множители. тогда получим, что

n 6 – 8 n 4 + 16 n 2 = n 2 · ( n 4 – 8 n 2 + 16 ) = n 2 · ( n 2 – 4 ) 2 = = n 2 · ( n – 2 ) 2 · ( n + 2 ) 2

Пусть m будет целым числом. Отсюда имеем, что n = 9 · m даст выражение вида n 2 · ( n – 2 ) 2 · ( n + 2 ) 2 = ( 9 m ) 2 · ( 9 m – 2 ) 2 · ( 9 m + 2 ) 2 . Так как имеется множитель 9 , то очевидно, что выражение поделится на 9 .

Если выражение вида n = 9 · m + 1 , то получим, что

n 2 · ( n – 2 ) 2 · ( n + 2 ) 2 = ( 9 m + 1 ) 2 · ( 9 m – 1 ) 2 · ( 9 m + 3 ) 2 = = 9 m + 1 2 · 9 m – 1 2 · 9 · 3 m + 1 2

Данное произведение поделится на 9 , так как есть множитель 9 . Таким же образом проверяется выражение вида n 2 · ( n – 2 ) 2 · ( n + 2 ) 2 при n = 9 · m + 2 , n = 9 · m + 3 , … , n = 9 · m + 8

Отсюда видно, что делимость на 9 доказана, значит, выражение делится на 9 при любом значении n .

Рассмотрим пример при помощи метода математической индукции.

Доказать, что выражение 4 n + 6 n – 1 делится на 9 при любом значении n .

Чтобы доказать делимость на 9 , необходимо использовать формулу математической индукции.

Когда n = 1 , то выражение 4 n + 6 n – 1 равняется 9 , значит и делится на 9 . Если предположить, что n = k , тогда выражение запишется так 4 k + 6 k – 1 . Оно тоже делится на 9 .

По предыдущему шагу понятно, что 4 n + 6 n – 1 будет делиться на число 9 при n=k+1.

4 k – 1 + 6 · ( k + 1 ) – 1 = = 4 · 4 k + 6 k + 5 = = 4 · ( 4 k + 6 k – 1 ) – 18 k + 9 = = 4 · ( 4 k + 6 k – 1 ) – 9 · ( 2 k – 1 )

Тогда из разности вида 4 · 4 k + 6 k – 1 видно, что она делится на 9 . Предыдущий шаг показал, что 4 k + 6 k – 1 делится на 9 также, как и 9 · ( 2 k – 1 ) . Отсюда получаем, что вся разность поделится на 9 . Можно говорить о том, что выражение 4 n + 6 n – 1 при n = k + 1 будет делиться на 9 .

Данное задание было решено при помощи метода математической индукции. Получили в результате, что заданное выражение поделится на 9 при любом целом значении n .

Источники:

http://www.nado5.ru/e-book/priznaki-delimosti-na-3-i-na-9
http://www.cleverstudents.ru/divisibility/divisibility_rule_for_9.html
http://zaochnik.com/spravochnik/matematika/delimost/priznak-delimosti-na-9/