Апории зенона дихотомия читать. Апории зенона элейского
Содержание
Апории Зенона и проблема движения
НАСТРОЙКИ.




СОДЕРЖАНИЕ.
СОДЕРЖАНИЕ

Апории Зенона и проблема движения
Нашей целью будет не реконструкция зеноновских аргументов, а стремление понять с точки зрения современной науки, на какие реальные трудности в анализе движения указал Зенон Элейский. Именно указал, поскольку о попытке приписать непосредственно Зенону современную постановку проблем движения не может быть и речи. Кстати говоря, эта постановка в логико-философской литературе не отличается единством. Нередко ответственность за парадоксы движения возлагается на неточность и размытость используемых понятий [1]. Уточним понятия – парадоксы исчезнут. Мы с этим не согласны. Апории Зенона касаются самих основ человеческого миропонимания. Они требуют не просто уточнения понятий, а выбора философской платформы объяснения реальности. Поскольку дело построения таких платформ не может быть завершено, пока существует мыслящий разум, на выборе одной из них лежит печать неизбежной исторической ограниченности. Сказанное, разумеется, в полной мере относится и к построениям в данной статье. Но сегодня, несомненно, мы понимаем и знаем больше, чем два с половиной тысячелетия назад, а завтра, возможно, удастся продвинуться вперед еще дальше [2].
Начнем рассмотрение зеноновских затруднений с апорий о движении.
Ахилл и черепаха
Ахилл – герой и, как бы мы сейчас сказали, выдающийся спортсмен. Черепаха, как известно, одно из самых медлительных животных. Тем не менее Зенон утверждал, что Ахилл проиграет черепахе состязание в беге. Примем следующие условия. Пусть Ахилла отделяет от финиша расстояние 1, а черепаху – ?. Двигаться Ахилл и черепаха начинают одновременно. Пусть для определенности Ахилл бежит в 2 раза быстрее черепахи. Тогда, пробежав расстояние ?, Ахилл обнаружит, что черепаха успела за то же время преодолеть отрезок ? и по-прежнему находится впереди героя. Далее картина повторяется: пробежав четвертую часть пути, Ахилл увидит черепаху на одной восьмой части пути впереди себя и т. д. Следовательно, всякий раз, когда Ахилл преодолевает отделяющее его от черепахи расстояние, последняя успевает уползти от него и по-прежнему остается впереди. Таким образом, Ахилл никогда не догонит черепаху. Начав движение, Ахилл никогда не сможет его завершить.
Знающие математический анализ обычно указывают, что ряд
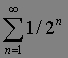
сходится к 1. Поэтому, дескать, Ахилл преодолеет весь путь за конечный промежуток времени и, безусловно, обгонит черепаху [3]. Но вот что пишут по данному поводу Д. Гильберт и П. Бернайс:
“Обычно этот парадокс пытаются обойти рассуждением о том, что сумма бесконечного числа этих временных интервалов все-таки сходится и, таким образом, дает конечный промежуток времени. Однако это рассуждение абсолютно не затрагивает один существенно парадоксальный момент, а именно парадокс, заключающийся в том, что некая бесконечная последовательность следующих друг за другом событий, последовательность, завершаемость которой мы не можем себе даже представить (не только физически, но хотя бы в принципе), на самом деле все-таки должна завершиться” [4] .
Принципиальная незавершаемость данной последовательности заключается в том, что в ней отсутствует последний элемент . Всякий раз, указав очередной член последовательности, мы можем указать и следующий за ним. Интересное замечание, также указывающее на парадоксальность ситуации, встречаем у Г. Вейля:
“Представим себе вычислительную машину, которая выполняла бы первую операцию за ? минуты, вторую – за ? минуты, третью – за ? минуты и т. д. Такая машина могла бы к концу первой минуты “пересчитать” весь натуральный ряд (написать, например, счетное число единиц). Ясно, что работа над конструкцией такой машины обречена на неудачу. Так почему же тело, вышедшее из точки А, достигает конца отрезка В, “отсчитав” счетное множество точек А1, А2,…, Аn,…?” [5]
Древние греки тем более не могли себе представить завершенную бесконечную совокупность. Поэтому вывод Зенона о том, что движение из-за необходимости “пересчитать” бесконечное число точек не может закончиться, еще тогда произвел большое впечатление. На схожих аргументах основывается апория о невозможности начать движение.
Рассуждения очень простое. Для того, чтобы пройти весь путь, движущееся тело сначала должно пройти половину пути, но чтобы преодолеть эту половину, надо пройти половину половины и т. д. до бесконечности. Иными словами, при тех же условиях, что и в предыдущем случае, мы будем иметь дело с перевернутым рядом точек: (?) n ,…, (?) 3 , (?) 2 , (?) 1 . Если в случае апории Ахилл и черепаха соответствующий ряд не имел последней точки, то в Дихотомии этот ряд не имеет первой точки. Следовательно, заключает Зенон, движение не может начаться. А поскольку движение не только не может закончиться, но и не может начаться, движения нет. Существует легенда, о которой вспоминает А. С. Пушкин в стихотворении «Движение»:
Движенья нет, сказал мудрец брадатый.
Другой смолчал и стал пред ним ходить.
Сильнее бы не мог он возразить;
Хвалили все ответ замысловатый.
Но, господа, забавный случай сей
Другой пример на память мне приводит:
Ведь каждый день пред нами солнце ходит,
Однако ж прав упрямый Галилей.
Действительно, согласно легенде, один из философов так и “возразил” Зенону. Зенон велел бить его палками: ведь он не собирался отрицать чувственное восприятие движения. Он говорил о его немыслимости , о том, что строгое размышление о движении приводит к неразрешимым противоречиям. Поэтому, если мы хотим избавиться от апорий в надежде, что это вообще возможно (а Зенон как раз считал, что невозможно), то мы должны прибегать к теоретическим аргументам, а не ссылаться на чувственную очевидность. Рассмотрим одно любопытное теоретическое возражение, которое было выдвинуто против апории Ахилл и черепаха .
“Представим себе, что по дороге в одном направлении движутся быстроногий Ахилл и две черепахи, из которых Черепаха-1 несколько ближе к Ахиллу, чем Черепаха-2. Чтобы показать, что Ахилл не сможет перегнать Черепаху-1, рассуждаем следующим образом. За то время, как Ахилл пробежит разделяющее их вначале расстояние, Черепаха-1 успеет уползти несколько вперед, пока Ахилл будет пробегать этот новый отрезок, она опять-таки продвинется дальше, и такое положение будет бесконечно повторяться. Ахилл
Апории Зенона
Проблема бесконечности и развитие античной диалектики
Зенон выдвинул ряд парадоксальных положений, которые получили название апорий («апория» в переводе с греческого означает «затруднение», «безвыходное положение»). С их помощью он хотел доказать, что бытие едино и неподвижно, а множественность и движение не могут быть мыслимы без противоречия, и потому они не суть бытие.
Первая из апорий — «Дихотомия» (что в переводе с греческого означает «деление пополам») доказывает невозможность мыслить движение. Зенон рассуждает так: чтобы пройти какое бы то ни было, пусть самое малое расстояние, надо сначала пройти его половину и т. д. без конца, поскольку любой отрезок линии можно делить до бесконечности. И в самом деле, если непрерывная величина (в данном случае — отрезок линии) мыслится как актуально данное бесконечное множество точек, то «пройти», «просчитать» все эти точки ни в какой конечный отрезок времени невозможно.
На том же допущении актуальной бесконечности элементов непрерывной величины основана и другая апория Зенона — «Ахиллес и черепаха». Зенон доказывает, что быстроногий Ахиллес никогда не сможет догнать черепаху, потому что, когда он преодолеет разделяющее их расстояние, черепаха проползет еще немного, и так всякий раз до бесконечности.
В третьей апории — «Стрела» — Зенон доказывает, что летящая стрела на самом деле покоится и, значит, движения опятьтаки на самом деле нет. Он разлагает непрерывность времени на сумму дискретных (неделимых) моментов, отдельных «теперь», а непрерывность пространства — на сумму отдельных неделимых отрезков. В каждый момент времени стрела, согласно Зенону, занимает определенное место, равное ее величине. Но это означает, что она в каждый момент неподвижно покоится, ибо движение, будучи непрерывным, предполагает, что предмет занимает место большее, чем он сам. Значит, движение можно мыслить только как сумму состояний покоя, и, стало быть, никакого движения нет, что и требовалось доказать. Таков результат, вытекающий из допущения, что протяженность состоит из суммы неделимых «мест», а время — из суммы неделимых мгновений. Движение ведь предполагает бесконечную делимость как пространства, так и времени.
Таким образом, как из допущения бесконечной делимости (которая, видимо, по Зенону, предполагает актуально бесконечное множество «точек» в любом отрезке), так и из допущения неделимости отдельных моментов времени Зенон делает один и тот же вывод: ни множество, ни движение не могут быть мыслимы без противоречия, а поскольку для элеатов бытие и мышление — одно и то же, тождественны, то движение и множественность не существует поистине, а только во мнении.
Парадоксы Зенона нередко рассматривались как софизмы, сбивающие людей с толку и ведущие к скептицизму. Характерно одно из опровержений Зенона философом Антисфеном. Выслушав аргументы Зенона, Антисфен встал и начал ходить, полагая, что доказательство действием сильнее всякого словесного возражения.
Несмотря на то что с точки зрения здравого смысла апории Зенона могут восприниматься как софизмы, на самом деле это — не просто игра ума: впервые в истории человеческого мышления здесь обсуждаются проблемы непрерывности и бесконечности. Зенон сформулировал вопрос о природе континуума, который является одним из «вечных вопросов» для человеческого ума.
Апории Зенона сыграли важную роль в развитии античной диалектики, как и античной науки, особенно логики и математики. Диалектика единого и многого, конечного и бесконечного составляет одну из наиболее важных заслуг Платона, в чьих диалогах мы находим классические образцы древнегреческой диалектики. Интересно, что понятие актуально бесконечного, введенное Зеноном для того, чтобы с его помощью доказать от противного основные положения онтологии Парменида, было исключено из употребления как в греческой философии (его не признавали ни Платон, ни Аристотель), так и в греческой математике. И та, и другая оперировала понятием потенциальной бесконечности, то есть бесконечной делимости величин, но не признавала их составленности из бесконечно большого числа актуально данных элементов.
Итак, в понятии бытия, как его осмыслили элеаты, содержится три момента: 1) бытие есть, а небытия нет; 2) бытие едино, неделимо; 3) бытие познаваемо, а небытие непознаваемо: его нет для разума, а значит, оно не существует.
Понятие единого играло важную роль также у пифагорейцев. Последние объясняли сущность всех вещей с помощью чисел и их соотношений, тем самым способствуя становлению и развитию древнегреческой математики. Началом числа у пифагорейцев выступало единое, или единица («монада»). Определение единицы, как его дает Евклид в VII книге «Начал», восходит к пифагорейскому: «Единица есть то, через что каждое из существующих считается единым». Единое, согласно пифагорейскому учению, по своему статусу выше множественности; оно служит началом определенности, дает всему предел, как бы стягивая, собирает множественное. А там, где налицо определенность, только и возможно познание: неопределенное — непознаваемо.
Апории Зенона Элейского
«Дихотомия»
Один из известнейших доводов Зенона об отсутствии движения гласит: «В конечный промежуток времени нельзя пройти бесконечное число отрезков, что означает невозможность начала самого движения».
Суть данного высказывания состоит в следующем. Если существует некий отрезок А-В, то чтобы попасть из точки А в точку В, нужно сначала добраться до точки С, которая будет серединой отрезка А-В. А чтобы достичь точки С, необходимо сперва попасть в точку D, являющуюся серединой А-С, и так будет продолжаться бесконечно. Из этого следует, что движение не начнется никогда, так как никогда не будет найден конечный пункт даже бесконечно малого смещения.
К данной апории в своих работах обращались многие философы, в том числе Аристотель, Гегель и Ленин, причем они не поддерживали точку зрения Зенона, а наоборот, приводили аргументы в пользу неверности утверждения. Так, Аристотель писал, что «…пространство и время бесконечно делимы в возможности, но не бесконечно разделены в действительности». Гегель, развивая мысль Аристотеля, утверждал, что делимость есть не необходимость, а лишь возможность деления.
«Ахиллес и черепаха»
На принципах, изложенных в «Дихотомии», базируется и еще одна апория, в которой Зенон рассказывает о том, что, чтобы Ахиллес догнал черепаху, необходимо, чтобы исчезло разделяющее их расстояние, а это невозможно.
Философ объясняет свою мысль тем, что если черепаха и Ахиллес начинают двигаться в одном направлении в одну и ту же секунду, но черепаха находится на каком-то расстоянии впереди, то пока Ахиллес будет преодолевать этот путь, черепаха продвинется на сколько-нибудь вперед, и дистанция будет бесконечно сокращаться, но в итоге между ними всегда будет оставаться не равное нулю расстояние.
Записав уравнения движений Ахиллеса и черепахи, можно выяснить, что в момент их предполагаемой встречи они должны пройти равное количество отрезков пути, а проходят разное: человек преодолевает один «лишний» отрезок. Это, с одной стороны, показывает формальную некорректность зеноновских утверждений, но, при этом, дает современным математикам и философам огромный простор для действий по доказательству или опровержению того, что часть равна целому.
Д. Гильберт и П. Бернайс замечают: «Обычно этот парадокс пытаются обойти рассуждением о том, что сумма бесконечного числа этих временных интервалов всё-таки сходится и, таким образом, даёт конечный промежуток времени. Однако это рассуждение абсолютно не затрагивает один парадокс, заключающийся в том, что некая бесконечная последовательность следующих друг за другом событий, последовательность, завершаемость которой мы не можем себе даже представить (не только физически, но хотя бы в принципе), на самом деле всё-таки должна завершиться» Д. Гильберт, П. Бернайс «Основания математики. Теория доказательств», 1982.
Данная апория Зенона не переставала интересовать математиков и философов. Однако вплоть до наших дней существуют самые разнообразные мнения: от совершенно-пренебрежительного отношения до признания того, что она относятся к наиболее важным и трудным вопросам обоснования математики и физики.
Так, известному французскому математику Полю Леви парадокс об Ахиллесе и черепахе представляется очевидной нелепостью.
«Почему воображать себе, – пишет он, – что время остановит свой ход вследствие того, что некий философ занимается перечислением членов сходящегося ряда? Признаюсь, я никогда не понимал, как люди, в других отношениях вполне разумные, могут оказаться смущёнными этим парадоксом, и ответ, который я только что наметил, есть тот самый ответ, который я дал, когда мне было одиннадцать лет, старшему, рассказавшему мне этот парадокс, или, точнее, есть тот самый ответ, который я резюмировал тогда такой немногословной формулой: Этот грек был идиотом» Р. Levy, A propos du paradoxe et de la logique,. «Rev. Meta-phys. Morale», 1957, N 2, p. 130.
Источники:
http://booksonline.com.ua/view.php?book=160852
http://filosofka.ru/emergence/aporii-zenona/
http://studwood.ru/958719/filosofiya/aporii_zenona_eleyskogo














